MIMO
In radio, multiple-input and multiple-output, or MIMO (commonly pronounced my-moh or me-moh), is the use of multiple antennas at both the transmitter and receiver to improve communication performance. It is one of several forms of smart antenna technology. Note that the terms input and output refer to the radio channel carrying the signal, not to the devices having antennas.
MIMO technology has attracted attention in wireless communications, because it offers significant increases in data throughput and link range without additional bandwidth or increased transmit power. It achieves this by spreading the same total transmit power over the antennas to achieve an array gain that improves the spectral efficiency (more bits per second per hertz of bandwidth) or to achieve a diversity gain that improves the link reliability (reduced fading). Because of these properties, MIMO is an important part of modern wireless communication standards such as IEEE 802.11n (Wifi), 4G, 3GPP Long Term Evolution, WiMAX and HSPA+.
Contents |
History of MIMO
Background technologies
The earliest ideas in this field go back to work by A.R. Kaye and D.A. George (1970) and W. van Etten (1975, 1976). Jack Winters and Jack Salz at Bell Laboratories published several papers on beamforming related applications in 1984 and 1986.[1]
Principle
Arogyaswami Paulraj and Thomas Kailath proposed the concept of spatial multiplexing (SM) using MIMO in 1993. Their US Patent No. 5,345,599 on Spatial Multiplexing issued 1994[2] emphasized applications to wireless broadcast.
In 1996, Greg Raleigh and Gerard J. Foschini refined new approaches to MIMO technology, considering a configuration where multiple transmit antennas are co-located at one transmitter to improve the link throughput effectively.[3][4]
Bell Labs was the first to demonstrate a laboratory prototype of spatial multiplexing in 1998, where spatial multiplexing is a principal technology to improve the performance of MIMO communication systems.[5]
Wireless standards
In the commercial arena, Iospan Wireless Inc. developed the first commercial system in 2001 that used MIMO with Orthogonal frequency-division multiple access technology (MIMO-OFDMA). Iospan technology supported both diversity coding and spatial multiplexing. In 2005, Airgo Networks had developed an IEEE 802.11n precursor implementation based on their patents on MIMO. Following that in 2006, several companies (including at least Broadcom, Intel, and Marvell) have fielded a MIMO-OFDM solution based on a pre-standard for 802.11n WiFi standard. Also in 2006, several companies (Beceem Communications, Samsung, Runcom Technologies, etc.) have developed MIMO-OFDMA based solutions for IEEE 802.16e WiMAX broadband mobile standard. All upcoming 4G systems will also employ MIMO technology. Several research groups have demonstrated over 1 Gbit/s prototypes.
Functions of MIMO
MIMO can be sub-divided into three main categories, precoding, spatial multiplexing or SM, and diversity coding.
Precoding is multi-stream beamforming, in the narrowest definition. In more general terms, it is considered to be all spatial processing that occurs at the transmitter. In (single-layer) beamforming, the same signal is emitted from each of the transmit antennas with appropriate phase (and sometimes gain) weighting such that the signal power is maximized at the receiver input. The benefits of beamforming are to increase the received signal gain, by making signals emitted from different antennas add up constructively, and to reduce the multipath fading effect. In the absence of scattering, beamforming results in a well defined directional pattern, but in typical cellular conventional beams are not a good analogy. When the receiver has multiple antennas, the transmit beamforming cannot simultaneously maximize the signal level at all of the receive antennas, and precoding with multiple streams is used. Note that precoding requires knowledge of channel state information (CSI) at the transmitter.
Spatial multiplexing requires MIMO antenna configuration. In spatial multiplexing, a high rate signal is split into multiple lower rate streams and each stream is transmitted from a different transmit antenna in the same frequency channel. If these signals arrive at the receiver antenna array with sufficiently different spatial signatures, the receiver can separate these streams into (almost) parallel channels. Spatial multiplexing is a very powerful technique for increasing channel capacity at higher signal-to-noise ratios (SNR). The maximum number of spatial streams is limited by the lesser in the number of antennas at the transmitter or receiver. Spatial multiplexing can be used with or without transmit channel knowledge. Spatial multiplexing can also be used for simultaneous transmission to multiple receivers, known as space-division multiple access. By scheduling receivers with different spatial signatures, good separability can be assured.
Diversity Coding techniques are used when there is no channel knowledge at the transmitter. In diversity methods, a single stream (unlike multiple streams in spatial multiplexing) is transmitted, but the signal is coded using techniques called space-time coding. The signal is emitted from each of the transmit antennas with full or near orthogonal coding. Diversity coding exploits the independent fading in the multiple antenna links to enhance signal diversity. Because there is no channel knowledge, there is no beamforming or array gain from diversity coding.
Spatial multiplexing can also be combined with precoding when the channel is known at the transmitter or combined with diversity coding when decoding reliability is in trade-off.
Forms of MIMO
Multi-antenna types
Multi-antenna MIMO (or Single user MIMO) technology has been developed and implemented in some standards, e.g. 802.11n products.
- SISO/SIMO/MISO are degenerate cases of MIMO
- Multiple-input and single-output (MISO) is a degenerate case when the receiver has a single antenna.
- Single-input and multiple-output (SIMO) is a degenerate case when the transmitter has a single antenna.
- single-input single-output (SISO) is a radio system where neither the transmitter nor receiver have multiple antenna.
- Principal single-user MIMO techniques
- Bell Laboratories Layered Space-Time (BLAST), Gerard. J. Foschini (1996)
- Per Antenna Rate Control (PARC), Varanasi, Guess (1998), Chung, Huang, Lozano (2001)
- Selective Per Antenna Rate Control (SPARC), Ericsson (2004)
- Some limitations
- The physical antenna spacing are selected to be large; multiple wavelengths at the base station. The antenna separation at the receiver is heavily space constrained in hand sets, though advanced antenna design and algorithm techniques are under discussion. Refer to: Advanced MIMO
Multi-user types
Recently, the research on multi-user MIMO technology has been emerging. While full multi-user MIMO (or network MIMO) can have higher potentials, from its practicality the research on (partial) multi-user MIMO (or multi-user and multi-antenna MIMO) technology is more active.
- Multi-user MIMO (MU-MIMO)
- In recent 3GPP and WiMAX standards, MU-MIMO is being treated as one of candidate technologies adoptable in the specification by a lot of companies including Samsung, Intel, Qualcomm, Ericsson, TI, Huawei, Philips, Alcatel-Lucent, Freescale, et al. since MU-MIMO is more feasible to low complexity mobiles with small number of reception antennas than SU-MIMO with the high system throughput capability.
- PU2RC allows the network to allocate each antenna to the different users instead of allocating only single user as in single-user MIMO scheduling. The network can transmit user data through a codebook-based spatial beam or a virtual antenna. Efficient user scheduling, such as pairing spatially distinguishable users with codebook based spatial beams, are additionally discussed for the simplification of wireless networks in terms of additional wireless resource requirements and complex protocol modification. Recently, PU2RC is included the system description documentation (SDD) of IEEE 802.16m (WiMAX evolution to meet the ITU-R's IMT-Advance requirements).
- Enhanced multiuser MIMO: 1)Employ advanced decoding techniques, 2) Employ advanced precoding techniques
- SDMA represents either space-division multiple access or super-division multiple access where super emphasises that orthogonal division such as frequency and time division is not used but non-orthogonal approaches such as super-position coding are used.
- Cooperative MIMO (CO-MIMO)
- Utilizes distributed antennas which belong to other users.
- MIMO Routing
- Routing a cluster by a cluster in each hop, where the number of nodes in each cluster is larger or equal to one. MIMO routing is different from conventional (SISO) routing since conventional routing protocols route a node by a node in each hop.[6]
Applications of MIMO
Spatial multiplexing techniques makes the receivers very complex, and therefore it is typically combined with Orthogonal frequency-division multiplexing (OFDM) or with Orthogonal Frequency Division Multiple Access (OFDMA) modulation, where the problems created by multi-path channel are handled efficiently. The IEEE 802.16e standard incorporates MIMO-OFDMA. The IEEE 802.11n standard, released in October 2009, recommends MIMO-OFDM.
MIMO is also planned to be used in Mobile radio telephone standards such as recent 3GPP and 3GPP2 standards. In 3GPP, High-Speed Packet Access plus (HSPA+) and Long Term Evolution (LTE) standards take MIMO into account. Moreover, to fully support cellular environments MIMO research consortia including IST-MASCOT propose to develop advanced MIMO techniques, i.e., multi-user MIMO (MU-MIMO).
MIMO technology can be used in non-wireless communications systems. One example is the home networking standard ITU-T G.9963, which defines a powerline communications system that uses MIMO techniques to transmit multiple signals over multiple AC wires (phase, neutral and ground).
Mathematical description
In MIMO systems, a transmitter sends multiple streams by multiple transmit antennas. The transmit streams go through a matrix channel which consists of all 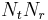 paths between the
paths between the 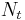 transmit antennas at the transmitter and
transmit antennas at the transmitter and 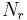 receive antennas at the receiver. Then, the receiver gets the received signal vectors by the multiple receive antennas and decodes the received signal vectors into the original information. A narrowband flat fading MIMO system is modelled as
receive antennas at the receiver. Then, the receiver gets the received signal vectors by the multiple receive antennas and decodes the received signal vectors into the original information. A narrowband flat fading MIMO system is modelled as
where 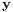 and
and 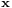 are the receive and transmit vectors, respectively, and
are the receive and transmit vectors, respectively, and 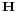 and
and 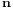 are the channel matrix and the noise vector, respectively. Referring to information theory, the ergodic channel capacity of MIMO systems where both the transmitter and the receiver have perfect instantaneous channel state information is[7]
are the channel matrix and the noise vector, respectively. Referring to information theory, the ergodic channel capacity of MIMO systems where both the transmitter and the receiver have perfect instantaneous channel state information is[7]
where 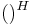 denotes Hermitian transpose and
denotes Hermitian transpose and  is the ratio between transmit power and noise power (i.e., transmit SNR). The optimal signal covariance
is the ratio between transmit power and noise power (i.e., transmit SNR). The optimal signal covariance 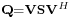 is achieved through singular value decomposition of the channel matrix
is achieved through singular value decomposition of the channel matrix 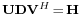 and an optimal diagonal power allocation matrix
and an optimal diagonal power allocation matrix 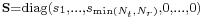 . The optimal power allocation is achieved through waterfilling,[8] that is
. The optimal power allocation is achieved through waterfilling,[8] that is
where 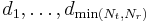 are the diagonal elements of
are the diagonal elements of 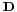 ,
, 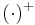 is zero if its argument is negative, and
is zero if its argument is negative, and  is selected such that
is selected such that 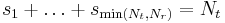 .
.
If the transmitter has only statistical channel state information, then the ergodic channel capacity will decrease as the signal covariance 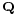 can only be optimized in terms of the average mutual information as[7]
can only be optimized in terms of the average mutual information as[7]
The spatial correlation of the channel have a strong impact on the ergodic channel capacity with statistical information.
If the transmitter has no channel state information it can select the signal covariance 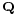 to maximize channel capacity under worst-case statistics, which means
to maximize channel capacity under worst-case statistics, which means 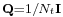 and accordingly
and accordingly
Depending on the statistical properties of the channel, the ergodic capacity is no greater than 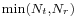 times larger than that of a SISO system.
times larger than that of a SISO system.
MIMO testing
MIMO signal testing focuses first on the transmitter/receiver system. The random phases of the sub-carrier signals can produce instantaneous power levels that cause the amplifier to compress, momentarily causing distortion and ultimately symbol errors. Signals with a high PAR (peak-to-average ratio) can cause amplifiers to compress unpredictably during transmission. OFDM signals are very dynamic and compression problems can be hard to detect because of their noise-like nature.
Knowing the quality of the signal channel is also critical. A channel emulator can simulate how a device performs at the cell edge, can add noise or can simulate what the channel looks like at speed. To fully qualify the performance of a receiver, a calibrated transmitter, such as a vector signal generator (VSG), and channel emulator can be used to test the receiver under a variety of different conditions. Conversely, the transmitter's performance under a number of different conditions can be verified using a channel emulator and a calibrated receiver, such as a vector signal analyzer (VSA).
Understanding the channel allows for manipulation of the phase and amplitude of each transmitter in order to form a beam. To correctly form a beam, the transmitter needs to understand the characteristics of the channel. This process is called channel sounding or channel estimation. A known signal is sent to the mobile device that enables it to build a picture of the channel environment. The phone then sends back the channel characteristics to the transmitter. The transmitter then can apply the correct phase and amplitude adjustments to form a beam directed at the mobile device. This is called a closed-loop MIMO system. For beamforming, it is required to adjust the phases and amplitude of each transmitter. In a beamformer optimized for spatial diversity or spatial multiplexing, each antenna element simultaneously transmits a weighted combination of two data symbols.[9]
MIMO literature
Principal researches
Papers by Gerard J. Foschini and Michael J. Gans,[10] Foschini[11] and Emre Telatar have shown that the channel capacity (a theoretical upper bound on system throughput) for a MIMO system is increased as the number of antennas is increased, proportional to the minimum number of transmit and receive antennas. This basic finding in information theory is what led to a spurt of research in this area. A text book by A. Paulraj, R. Nabar and D. Gore has published an introduction to this area.[12] Mobile Experts has published a research report which predicts the use of MIMO technology in 500 million PCs, tablets, and smartphones by 2016. link
Diversity-multiplexing tradeoff (DMT)
There exists a fundamental tradeoff between diversity and multiplexing in a MIMO system (Zheng and Tse, 2003) .[13]
Other applications
Given the nature of MIMO, it is not limited to wireless communication. It can be used for wire line communication as well. For example, a new type of DSL technology (Gigabit DSL) has been proposed based on Binder MIMO Channels.
Sampling theorem in MIMO systems
An important question which attracts the attention of engineers and mathematician is how to use the multi-output signals at the receiver to recover the multi-input signals at the transmitter. In Shang, Sun and Zhou (2007), sufficient and necessary conditions are established to guarantee the complete recovery of the multi-input signals. .[14]
See also
- Channel bonding
- Mimax
- Single-frequency network (SFN)
- WiMAX MIMO
- wifi
Intelligent antenna technology
Spatial techniques
- Antenna diversity
- Beamforming
- Channel state information
- Dirty paper coding (DPC)
- Precoding
- Space–time block code
- Space–time code
- Spatial multiplexing
- Multi-user MIMO
- 802.11
- 802.16
References
- ^ J. Salz, “Digital transmission over cross-coupled linear channels,” AT&T Technical Journal, vol. 64, no. 6, pp. 1147–1159, July–August 1985.
- ^ http://patft.uspto.gov/netacgi/nph-Parser?Sect2=PTO1&Sect2=HITOFF&p=1&u=%2Fnetahtml%2FPTO%2Fsearch-bool.html&r=1&f=G&l=50&d=PALL&RefSrch=yes&Query=PN%2F5345599
- ^ Gregory G. Raleigh and John M. Cioffi, “Spatio-temporal coding for wireless communication,” IEEE Transactions on Communications, vol. 46, no. 3, pp. 357–366, March 1998.
- ^ G. J. Foschini, “Layered space–time architecture for wireless communication in a fading environment when using multiple antennas,” Bell Labs Syst. Tech. J., vol. 1, p. 41–59, Autumn 1996.
- ^ G. D. Golden, G. J. Foschini, R. A. Valenzuela, and P. W. Wolniansky, “Detection algorithm and initial laboratory results using V-BLAST space–time communication architecture,” Electron. Lett., vol. 35, pp.~14–16, Jan. 1999.
- ^ S. Cui, A. J. Goldsmith, and A. Bahai (August, 2004). "Energy-efficiency of MIMO and Cooperative MIMO in Sensor Networks". IEEE J. Select. Areas of Commun. 22 (6): 1089–1098. doi:10.1109/JSAC.2004.830916.
- ^ a b D. Love, R. Heath, V. Lau, D. Gesbert, B. Rao and M. Andrews, An overview of limited feedback in wireless communication systems, IEEE Journal on Selected Areas Communications, vol 26, pp. 1341–1365, 2008.
- ^ D. Tse and P. Viswanath, Fundamentals of Wireless Communication, Cambridge University Press, 2005.
- ^ Agilent [1], Agilent MIMO Channel Modeling and Emulation Test Challenges, pg. 10, January 22, 2010, accessed September 16, 2011.
- ^ Gerard J. Foschini and Michael. J. Gans (January 1998). "On limits of wireless communications in a fading environment when using multiple antennas". Wireless Personal Communications 6 (3): 311–335. doi:10.1023/A:1008889222784.
- ^ Gerard J. Foschini (autumn 1996). "Layered space-time architecture for wireless communications in a fading environment when using multi-element antennas". Bell Labs Technical Journal 1 (2): 41–59. doi:10.1002/bltj.2015.
- ^ A. Paulraj, R. Nabar and D. Gore. Introduction to Space-time Communications.
- ^ L. Zheng and D. N. C. Tse (May 2003). "Diversity and multiplexing: A fundamental tradeoff in multiple-antenna channels". IEEE Trans. Inf. Th. 49 (5): 1073–1096. doi:10.1109/TIT.2003.810646.
- ^ Z. Shang, W. Sun and X. Zhou (January 2007). "Vector sampling expansions in shift invariant subspaces". Journal of Mathematical Analysis and Applications 325 (2): 898–919. doi:10.1016/j.jmaa.2006.02.033.
External links
Web sites
- GEDOMIS (GEneric hardware DemOnstrator for MIMO Systems)
- NIST UWB-MIMO Channel Propagation Measurements in the 2–8 GHz Spectrum
- D. Gesbert, M. Kountouris, R. W. Heath, Jr., C.-B. Chae, and T. Salzer, Shifting the MIMO Paradigm: From Single User to Multiuser Communications, IEEE Signal Processing Magazine, vol. 24, no. 5, pp. 36–46, Oct., 2007
- Links to suggested readings in MIMO - WCSP Group — University of South Florida (USF)
- Introduction to Wireless MIMO - Theory and Applications
- Introduction to Orthogonal Frequency Division Multiplexing (covers OFDM and MIMO radio configurations)
- Introduction to MIMO
- Computerworld QuickStudy MIMO
- Developing Strategies for MIMO Testing
- Meeting The Test Challenges Of 4G LTE
- The Basics Of OFDM
- MIMO: The Future Of Wireless: Test Challenges For WiMAX, HSPA+, And LTE
- OFDM Will Soon Be Dominant Form Of Digital Modulation
- The challenges of moving to MIMO systems
- RF test system tackles 4 × 4 MIMO signals
- Increasing Mobile Systems Raises RF Test Throughput Issues
- The Role Of EVM Measurements In Characterizing Amplifier Modulation Performance
- Industry Views: 4G Systems Bring New Design And Testing Challenges
- Test System Pushes MIMO Standards Into The Spotlight
- Instruments test MIMO data transmissions
- Literature review of MIMO
Books
- Claude Oestges, Bruno Clerckx, "MIMO Wireless Communications : From Real-world Propagation to Space-time Code Design," Academic, 2007.07.16, 448p, ISBN : 0123725356
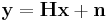
![C_\mathrm{perfect-CSI} = E\left[\max_{\mathbf{Q}; \, \mbox{tr}(\mathbf{Q}) \leq 1} \log_2 \det\left(\mathbf{I} %2B \rho \mathbf{H}\mathbf{Q}\mathbf{H}^{H}\right)\right] = E\left[\log_2 \det\left(\mathbf{I} %2B \rho \mathbf{D}\mathbf{S} \mathbf{D} \right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/3321ca77bd0ff0e22488355983e63162.png)
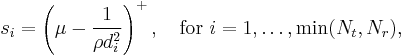
![C_\mathrm{statistical-CSI} = \max_{\mathbf{Q}} E\left[\log_2 \det\left(\mathbf{I} %2B \rho \mathbf{H}\mathbf{Q}\mathbf{H}^{H}\right)\right].](/2012-wikipedia_en_all_nopic_01_2012/I/24dc947ca96b5c7d1881848c7e5b826b.png)
![C_\mathrm{no-CSI} = E\left[\log_2 \det\left(\mathbf{I} %2B \frac{\rho}{N_t}\mathbf{H}\mathbf{H}^{H}\right)\right].](/2012-wikipedia_en_all_nopic_01_2012/I/c813e60a5fd14ff0aaa7249a91ee8edb.png)