Milü

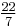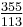The name Milü (Chinese: 密率; pinyin: mì lǜ; literally "detailed (approximation) ratio"), also known as Zulü (Zu's ratio), is given to an approximation to π (Pi) found by Chinese mathematician and astronomer Zu Chongzhi. He computed π to be between 3.1415926 and 3.1415927 and gave two rational approximations of π, $\tfrac{22}{7}$ and $\tfrac{355}{113}$ , naming them respectively Yuelü 约率 (literally "approximate ratio") and Milü.

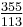$\tfrac{355}{113}$ is by far the best rational approximation of π with a denominator of four digits or fewer, being accurate to 6 decimal places. It is within 0.000009% of the value of π, or in terms of common fractions overestimates π by less than 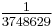$\tfrac{1}{3748629}$ . The next rational number (ordered by size of denominator) that is a better rational approximation of π is 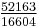$\tfrac{52163}{16604}$ , still only correct to 6 decimal places. 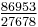To be accurate to 7 decimal places, one needs to go as far as $\tfrac{86953}{27678}$ .

$\begin{align}\pi & \approx 3.141\ 592\ 653\ 5\dots \\ \\ \frac{355}{113} & \approx 3.141\ 592\ 920\ 3\dots \\ \\ \frac{52163}{16604} & \approx 3.141\ 592\ 387\ 4\dots \\ \\ \frac{86953}{27678} & \approx 3.141\ 592\ 600\ 6\dots\end{align}$

An easy mnemonic helps memorize this useful fraction by writing down each of the first three odd numbers twice: 1 1 3 3 5 5, then dividing the decimal number represented by the last 3 digits by the decimal number given by the first three digits.

Zu's contemporary calendarist and mathematician He Chengtian invented a fraction interpolation method called "harmonization of the divisor of the day" to obtain a closer approximation by iteratively adding the numerators and denominators of a "weak" fraction and a "strong" fraction.^[1] Zu Chongzhi's approximation 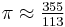$\pi \approx \tfrac{355}{113}$ can be obtained with He's method^[2]

References

^ Jean claude Martzloff, A History of Chinese Mathematics p281
^ Wu Wenjun ed Grand Series of History of Chinese Mathematics vol 4 p125

Milü

See also

References