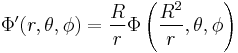Method of image charges
The method of image charges (also known as the method of images and method of mirror charges) is a basic problem-solving tool in electrostatics. The name originates from the replacement of certain elements in the original layout with imaginary charges, which replicates the boundary conditions of the problem (see Dirichlet boundary conditions or Neumann boundary conditions).
Contents |
Uniqueness theorem
Any uniqueness theorem says that an object satisfying some set of given conditions or properties is the only such object that exists; it is uniquely determined by the specified conditions.
To illustrate, draw a closed loop to define a region inside and a surface on the line. If:
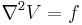 within the region and V = g on the surface
within the region and V = g on the surface
then 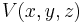 is unique (given constant f and g).
is unique (given constant f and g).
In this case of image charges we can use the uniqueness theorem to say that provided the boundary conditions laid out by the problem are satisfied, any element can be replaced and then that this is the only alternative arrangement.
The simplest example of a use of this method is that in 2-dimensional space of a point charge, with charge +q, located at (0, a) above an 'infinite' grounded (ie: V = 0) conducting plate, lying along the x-axis. Deriving any results from this setup, such as the charge distribution on the plate, or the force felt by the point charge, is not trivial.
In order to simplify this problem, we may replace the plate of equipotential with a charge, located at (0, −a) and with charge −q. This arrangement will produce the same electric field at any point for which y > 0 (ie: above the conducting plate), and satisfies the boundary condition, that the potential along the plate must be zero. This new setup is depicted below.
This situation is equivalent to the original setup, and so calculating the force on the real charge is now trivial, by use of Coulomb's law. Finding the charge density on the plate is less obvious, but still easily attainable by using Gauss' law. In order to use Gauss' law, we now extend this case to three dimensions, so that we may construct 2-dimensional Gaussian surfaces (ie: the plate now lies on the xz-plane).
The potential, in cylindrical coordinates, at any point in space due to two point charges of charge +q at +a and -q at -a on the z-axis is simply:
And because of the uniqueness theorem, this turns out to be the only solution to this problem.
The surface charge on the grounded plane is given by
Which, after simplifying, ends up being:
In addition, the total charge induced on the conducting plane will be the integral of the charge density over the entire plane, so:
So the total charge induced on the plane turns out to be simply -q.
Extension
This method can be extended to two or more charges, replacing the plate with the 'image charge' of each real charge. As the total electrostatic potential is equal to the scalar sum of the potentials, at any point on the xz plane the potential of any real charge will cancel with that of its image. Hence the potential anywhere on the plane will be zero, and the boundary condition satisfied.
The diagram to the right depicts a specific case of this extension, in which there are two (real) charges present, each a distance a above the plate.
If there is an electric dipole at a distance h from a grounded surface, inclined by an angle θ, you may substitute the surface by an inverse symmetric dipole.
Method of images for spheres
The method of images may be applied to a sphere as well (Tikhonov 1963). In fact, the case of image charges in a plane is a special case of the case of images for a sphere. Referring to the figure, we wish to find the potential inside a grounded sphere of radius R, centered at the origin, due to a point charge inside the sphere at position 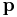 . In the figure, this is represented by the green point. Let q be the charge of this point. The image of this charge with respect to the grounded sphere is shown in red. It has a charge of q'=-qR/p and lies on a line connecting the center of the sphere and the inner charge at vector position
. In the figure, this is represented by the green point. Let q be the charge of this point. The image of this charge with respect to the grounded sphere is shown in red. It has a charge of q'=-qR/p and lies on a line connecting the center of the sphere and the inner charge at vector position 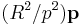 . It can be seen that the potential at a point specified by radius vector
. It can be seen that the potential at a point specified by radius vector 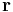 due to both charges alone is given by the sum of the potentials:
due to both charges alone is given by the sum of the potentials:
Multiplying through on the rightmost expression yields:
and it can be seen that on the surface of the sphere (i.e. when r=R), the potential vanishes. The potential inside the sphere is thus given by the above expression for the potential of the two charges. This potential will NOT be valid outside the sphere, since the image charge does not actually exist, but is rather "standing in" for the surface charge densities induced on the sphere by the inner charge at 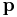 . The potential outside the grounded sphere will be determined only by the distribution of charge outside the sphere and will be independent of the charge distribution inside the sphere. If we assume for simplicity (without loss of generality) that the inner charge lies on the z-axis, then the induced charge density will be simply a function of the polar angle θ and is given by:
. The potential outside the grounded sphere will be determined only by the distribution of charge outside the sphere and will be independent of the charge distribution inside the sphere. If we assume for simplicity (without loss of generality) that the inner charge lies on the z-axis, then the induced charge density will be simply a function of the polar angle θ and is given by:
The total charge on the sphere may be found by integrating over all angles:
Note that the reciprocal problem is also solved by this method. If we have a charge q at vector position 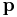 outside of a grounded sphere of radius R, the potential outside of the sphere is given by the sum of the potentials of the charge and its image charge inside the sphere. Just as in the first case, the image charge will have charge -qR/p and will be located at vector position
outside of a grounded sphere of radius R, the potential outside of the sphere is given by the sum of the potentials of the charge and its image charge inside the sphere. Just as in the first case, the image charge will have charge -qR/p and will be located at vector position 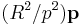 . The potential inside the sphere will be dependent only upon the true charge distribution inside the sphere.
. The potential inside the sphere will be dependent only upon the true charge distribution inside the sphere.
The image of an electric point dipole is a bit more complicated. If the dipole is pictured as two large charges separated by a small distance, then the image of the dipole will not only have the charges modified by the above procedure, but the distance between them will be modified as well. Following the above procedure, it is found that a dipole with dipole moment 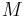 at vector position
at vector position 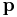 lying inside the sphere of radius R will have an image located at vector position
lying inside the sphere of radius R will have an image located at vector position 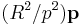 (i.e. the same as for the simple charge) and will have a simple charge of:
(i.e. the same as for the simple charge) and will have a simple charge of:
and a dipole moment of:
Method of Inversion
The method of images for a sphere leads directly to the method of inversion (Jackson 1962 p35). If we have a harmonic function of position 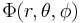 where
where 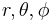 are the spherical coordinates of the position, then the image of this harmonic function in a sphere of radius R about the origin will be
are the spherical coordinates of the position, then the image of this harmonic function in a sphere of radius R about the origin will be
If the potential Φ arises from a set of charges of magnitude 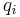 at positions
at positions 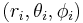 , then the image potential will be the result of a series of charges of magnitude
, then the image potential will be the result of a series of charges of magnitude 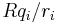 at positions
at positions 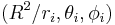 . It follows that if the potential Φ arises from a charge density
. It follows that if the potential Φ arises from a charge density 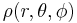 , then the image potential will be the result of a charge density
, then the image potential will be the result of a charge density 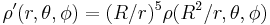 .
.
See also
- Kelvin transform
- Coulomb's law
- Divergence theorem
- Flux
- Gaussian surface
- Schwarz reflection principle
- Uniqueness theorem for Poisson's equation
Further reading
- Feynman, Richard; Leighton, Robert; Sands, Matthew (1989). Feynman Lectures on Physics, Mainly Electromagnetism and Matter. Addison-Wesley. ISBN 0-201-51003-0.
- James Jeans (1908) The Mathematical Theory of Electricity and Magnetism, Chapter 8, Cambridge University Press.
References
- Purcell, Edward Mills. Berkeley Physics Course, Vol-2: Electricity and Magnetism (2nd ed.). McGraw-Hill. An excellent introductory book that introduces the ideas of electromagnetism in a logically sound manner. Also contains beautiful diagrams.
- Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Tikhonov, A. N.; Samarskii, A. A. (1963). Equations of Mathematical Physics. New York: Dover Publications. ISBN 0-486-66422-8.
- Landau, L. D.; Lifshitz, E.M., Pitaevskii, L.P (1960). Electrodynamics of Continuous Media 2nd Edition. London: Elsevier. ISBN 978-0-7506-2634-7.
- Jackson, John David (1962). Classical Electrodynamics. John Wiley & Sons, Inc..
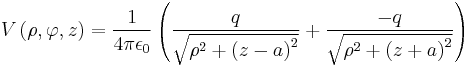
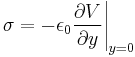
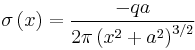
![\begin{align}
Q_t & = \int_0^{2\pi}\int_0^\infty \sigma\left(x\right)\, x\,d x\,d\theta \\[6pt]
& = \frac{-qa}{2\pi} \int_0^{2\pi}d\theta \int_0^\infty \frac{x\,d x}{\left(x^2 %2B a^2\right)^{3/2}} \\[6pt]
& = -q
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/8be6f9419f8a479442b427f0f9031910.png)
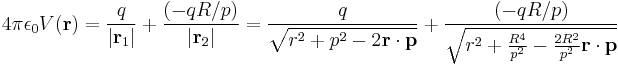
![V(\mathbf{r})=\frac{1}{4\pi \epsilon_0}\left[
\frac{q}{\sqrt{r^2%2Bp^2-2\mathbf{r}\cdot\mathbf{p}}}-\frac{q}{\sqrt{\frac{r^2p^2}{R^2}%2BR^2-2\mathbf{r}\cdot\mathbf{p}}}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/8f214324b002b45e5bcd3b8a5859155d.png)
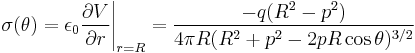
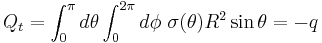
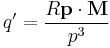
![\mathbf{M}'=R^3\left[
-\frac{\mathbf{M}}{p^3}
%2B\frac{2\mathbf{p}(\mathbf{p}\cdot\mathbf{M})}{p^5}
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/f921224744c42f83be22a1740d237eb6.png)