Mean-shift

Mean shift is a non-parametric feature-space analysis technique, a so-called mode seeking algorithm.[1] Application domains include clustering in computer vision and image processing.[2]

Contents

History

The mean shift procedure was originally presented in 1975 by Fukunaga and Hostetler.[3]

Overview

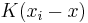Mean shift is a procedure for locating the maxima of a density function given discrete data sampled from that function.[1] It is useful for detecting the modes of this density.[1] This is an iterative method, and we start with an initial estimate x . Let a kernel function K(x_i - x) be given. This function determines the weight of nearby points for re-estimation of the mean. Typically we use the Gaussian kernel on the distance to the current estimate, 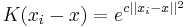K(x_i - x) = e^{c||x_i - x||^2} . The weighted mean of the density in the window determined by K is

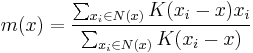
m(x) = \frac{ \sum_{x_i \in N(x)} K(x_i - x) x_i } {\sum_{x_i \in N(x)} K(x_i - x)}

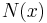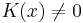where N(x) is the neighborhood of x , a set of points for which K(x) \neq 0 .

The mean-shift algorithm now sets 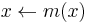x \leftarrow m(x) , and repeats the estimation until 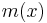m(x) converges.

Mean shift for visual tracking

The mean shift algorithm can be used for visual tracking. The simplest such algorithm would create a confidence map in the new image based on the color histogram of the object in the previous image, and use mean shift to find the peak of a confidence map near the object's old position. A few algorithms, such as Ensemble Tracking,[4] expand on this idea.

See also

References

  1. ^ a b c Cheng, Yizong (August 1995). "Mean Shift, Mode Seeking, and Clustering". IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE) 17 (8): 790–799. doi:10.1109/34.400568. 
  2. ^ Comaniciu, Dorin; Peter Meer (May 2002). "Mean Shift: A Robust Approach Toward Feature Space Analysis". IEEE Transactions on Pattern Analysis and Machine Intelligence (IEEE) 24 (5): 603–619. doi:10.1109/34.1000236. 
  3. ^ Fukunaga, Keinosuke; Larry D. Hostetler (January 1975). "The Estimation of the Gradient of a Density Function, with Applications in Pattern Recognition". IEEE Transactions on Information Theory (IEEE) 21 (1): 32–40. doi:10.1109/TIT.1975.1055330. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1055330. Retrieved 2008-02-29. 
  4. ^ Avidan, Sai (2005). "Ensemble Tracking". 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05) (San Diego, California: IEEE) 2. ISBN 0-7695-2372-2. 

Code implementations