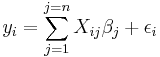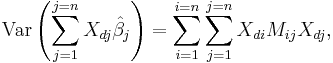Mean and predicted response
In linear regression mean response and predicted response are values of the dependent variable calculated from the regression parameters and a given value of the independent variable. The values of these two responses are the same, but their calculated variances are different.
Contents |
Straight line regression
In straight line fitting the model is
where 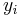 is the response variable,
is the response variable,  is the explanatory variable, εi is the random error, and
is the explanatory variable, εi is the random error, and  and
and  are parameters. The predicted response value for a given explanatory value, xd, is given by
are parameters. The predicted response value for a given explanatory value, xd, is given by
while the actual response would be
Expressions for the values and variances of 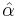 and
and 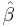 are given in linear regression.
are given in linear regression.
Mean response is an estimate of the mean of the y population associated with xd, that is 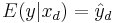 . The variance of the mean response is given by
. The variance of the mean response is given by
This expression can be simplified to
To demonstrate this simplification, one can make use of the identity
The predicted response distribution is the predicted distribution of the residuals at the given point xd. So the variance is given by
The second part of this expression was already calculated for the mean response. Since 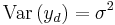 (a fixed but unknown parameter that can be estimated), the variance of the predicted response is given by
(a fixed but unknown parameter that can be estimated), the variance of the predicted response is given by
Confidence intervals
The 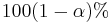 confidence intervals are computed as
confidence intervals are computed as 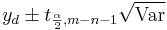 . Thus, the confidence interval for predicted response is wider than the interval for mean response. This is expected intuitively – the variance population of
. Thus, the confidence interval for predicted response is wider than the interval for mean response. This is expected intuitively – the variance population of  values does not shrink when one samples from it, because the random variable εi does not decrease, but the variance mean of the
values does not shrink when one samples from it, because the random variable εi does not decrease, but the variance mean of the  does shrink with increased sampling, because the variance in
does shrink with increased sampling, because the variance in 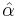 and
and 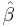 decrease, so the mean response (predicted response value) becomes closer to
decrease, so the mean response (predicted response value) becomes closer to 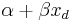 .
.
This is analogous to the difference between the variance of a population and the variance of the sample mean of a population: the variance of a population is a parameter and does not change, but the variance of the sample mean decreases with increased samples.
General linear regression
The general linear model can be written as
Therefore since 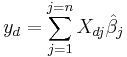 the general expression for the variance of the mean response is
the general expression for the variance of the mean response is
where M is the covariance matrix of the parameters, given by
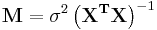 .
.
References
Draper, N.R., Smith, H. (1998) Applied Regression Analysis. Wiley. ISBN 0-471-17082-8
|
||||||||||||||||||||||||||||||||||||||||||||||
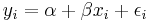
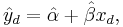
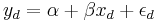
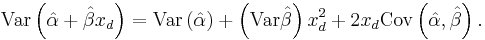
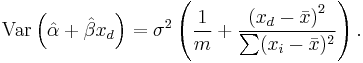
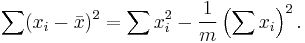
![\text{Var}\left(y_d - \left[\hat{\alpha} %2B \hat{\beta}x_d\right]\right) = \text{Var}\left(y_d\right) %2B \text{Var}\left(\hat{\alpha} %2B \hat{\beta}x_d\right) .](/2012-wikipedia_en_all_nopic_01_2012/I/b187a3794370a0e3859f1ac35effaadf.png)
![\text{Var}\left(y_d - \left[\hat{\alpha} %2B \hat{\beta}x_d\right]\right) = \sigma^2 %2B \sigma^2\left(\frac{1}{m} %2B \frac{\left(x_d - \bar{x}\right)^2}{\sum (x_i - \bar{x})^2}\right) = \sigma^2\left(1%2B\frac{1}{m} %2B \frac{\left(x_d - \bar{x}\right)^2}{\sum (x_i - \bar{x})^2}\right) .](/2012-wikipedia_en_all_nopic_01_2012/I/f4e4d294214cfcaac192dea673554fb2.png)