Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability. See Singularity theory for general discussion of the geometric theory, which only covers some aspects.
For example, the function
on the real line has a singularity at x = 0, where it seems to "explode" to ±∞ and is not defined. The function g(x) = |x| (see absolute value) also has a singularity at x = 0, since it is not differentiable there. Similarly, the graph defined by y2 = x also has a singularity at (0,0), this time because it has a "corner" (vertical tangent) at that point.
The algebraic set defined by y2 = x2 in the (x, y) coordinate system has a singularity (singular point) at (0, 0) because it does not admit a tangent there.
Contents |
Real analysis
In real analysis singularities are also called discontinuities. There are three kinds: type I, which has two sub-types, and type II, which also can be divided into two subtypes, but normally is not.
To describe these types, suppose that  is a function of a real argument
is a function of a real argument  , and for any value of its argument, say
, and for any value of its argument, say  , the symbols
, the symbols 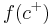 and
and 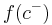 are defined by:
are defined by:
 , constrained by
, constrained by  and
and
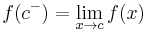 , constrained by
, constrained by 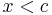 .
.
The limit 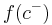 is called the left-handed limit, and
is called the left-handed limit, and 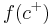 is called the right-handed limit. The value
is called the right-handed limit. The value 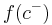 is the value that the function
is the value that the function  tends towards as the value
tends towards as the value  approaches
approaches  from below, and the value
from below, and the value 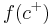 is the value that the function
is the value that the function  tends towards as the value
tends towards as the value  approaches
approaches  from above, regardless of the actual value the function has at the point where
from above, regardless of the actual value the function has at the point where 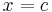 .
.
There are some functions for which these limits do not exist at all. For example the function
does not tend towards anything as  approaches
approaches 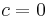 . The limits in this case are not infinite, but rather undefined: there is no value that
. The limits in this case are not infinite, but rather undefined: there is no value that 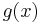 settles in on. Borrowing from complex analysis, this is sometimes called an essential singularity.
settles in on. Borrowing from complex analysis, this is sometimes called an essential singularity.
- A point of continuity, which is not a singularity, is a value of
 for which
for which 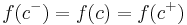 , as one usually expects. All the values must be finite.
, as one usually expects. All the values must be finite. - A type I discontinuity occurs when both
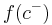 and
and 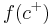 exist and are finite, but one of three conditions also apply:
exist and are finite, but one of three conditions also apply: 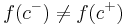 ;
; 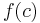 does not exist for that value of
does not exist for that value of  ; or
; or 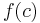 does not match the value that the two limits tend towards. Two subtypes occur:
does not match the value that the two limits tend towards. Two subtypes occur:
- A jump discontinuity occurs when
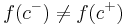 , regardless of whether
, regardless of whether 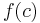 exists, and regardless of what value it might have if it does exist.
exists, and regardless of what value it might have if it does exist. - A removable discontinuity occurs when
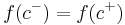 , but either the value of
, but either the value of 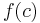 does not match the limits, or the function does not exist at the point
does not match the limits, or the function does not exist at the point 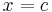 .
.
- A jump discontinuity occurs when
- A type II discontinuity occurs when either
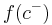 or
or 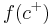 does not exist (possibly both). This has two subtypes, which are usually not considered separately:
does not exist (possibly both). This has two subtypes, which are usually not considered separately:
- An infinite discontinuity is the special case when either the left hand or right hand limit does not exist specifically because it is infinite, and the other limit is either also infinite or is some well defined finite number.
- An essential singularity is a term borrowed from complex analysis (see below). This is the case when either one or the other limits
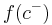 or
or 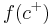 does not exist, but not because it is an infinite discontinuity. Essential singularities approach no limit, not even if legal answers are extended to include
does not exist, but not because it is an infinite discontinuity. Essential singularities approach no limit, not even if legal answers are extended to include 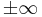 .
.
In real analysis, a singularity or discontinuity is a property of a function alone. Any singularities that may exist in the derivative of a function are considered as belonging to the derivative, not to the original function.
Coordinate singularities
A coordinate singularity (or coördinate singularity) occurs when an apparent singularity or discontinuity occurs in one coordinate frame, which can be removed by choosing a different frame. An example is the apparent singularity at the 90 degree latitude in spherical coordinates. An object moving due north (for example, along the line 0 degrees longitude) on the surface of a sphere will suddenly experience an instantaneous change in longitude at the pole (in the case of the example, jumping from longitude 0 to longitude 180 degrees). This discontinuity, however, is only apparent; it is an artifact of the coordinate system chosen, which is singular at the poles. A different coordinate system would eliminate the apparent discontinuity, e.g. by replacing latitude/longitude with n-vector.
Complex analysis
In complex analysis there are four classes of singularities, described below. Suppose U is an open subset of the complex numbers C, and the point a is an element of U, and f is a complex differentiable function defined on some neighborhood around a, excluding a: U \ {a}.
- Isolated singularities: Suppose the function f is not defined at a, although it does have values defined on U \ {a}.
- The point a is a removable singularity of f if there exists a holomorphic function g defined on all of U such that f(z) = g(z) for all z in U \ {a}. The function g is a continuous replacement for the function f.
- The point a is a pole or non-essential singularity of f if there exists a holomorphic function g defined on U and a natural number n such that f(z) = g(z) / (z − a)n for all z in U \ {a}. The derivative at a non-essential singularity may or may not exist. If g(a) is nonzero, then we say that a is a pole of order n.
- The point a is an essential singularity of f if is neither a removable singularity nor a pole. The point a is an essential singularity if and only if the Laurent series has infinitely many powers of negative degree.
- Branch points are generally the result of a multi-valued function, such as
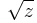 or
or 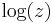 being defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The location and shape of most of the branch cut is usually a matter of choice, with perhaps only one point (like
being defined within a certain limited domain so that the function can be made single-valued within the domain. The cut is a line or curve excluded from the domain to introduce a technical separation between discontinuous values of the function. When the cut is genuinely required, the function will have distinctly different values on each side of the branch cut. The location and shape of most of the branch cut is usually a matter of choice, with perhaps only one point (like 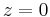 for
for 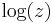 ) which is fixed in place.
) which is fixed in place.
Finite-time singularity
A finite-time singularity occurs when one input variable is time, and an output variable increases towards infinite at a finite time. These are important in kinematics and PDEs – infinites do not occur physically, but the behavior near the singularity is often of interest. Mathematically the simplest finite-time singularities are power laws for various exponents, 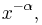 of which the simplest is hyperbolic growth, where the exponent is (negative) 1:
of which the simplest is hyperbolic growth, where the exponent is (negative) 1: 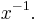 More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses
More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses 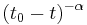 (using t for time, reversing direction to
(using t for time, reversing direction to 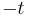 so time increases to infinity, and shifting the singularity forward from 0 to a fixed time
so time increases to infinity, and shifting the singularity forward from 0 to a fixed time 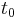 ).
).
An example would be the bouncing motion of an inelastic ball on a plane. If idealized motion is considered, in which the same fraction of kinetic energy is lost on each bounce, the frequency of bounces becomes infinite as the ball comes to rest in a finite time. Other examples of finite-time singularities include the Painlevé paradox in various forms (for example, the tendency of a chalk to skip when dragged across a blackboard), and how the precession rate of a coin spun on a flat surface accelerates towards infinite, before abruptly stopping (asd studied using the Euler's Disk toy).
Hypothetical examples include Heinz von Foerster's facetious "Doomsday's Equation" (simplistic models yield infinite human population in finite time).
Algebraic geometry and commutative algebra
In algebraic geometry and commutative algebra, a singularity is a prime ideal whose localization is not a regular local ring (alternately a point of a scheme whose stalk is not a regular local ring). For example, 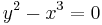 defines an isolated singular point (at the cusp)
defines an isolated singular point (at the cusp) 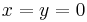 . The ring in question is given by
. The ring in question is given by
The maximal ideal of the localization at 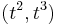 is a height one local ring generated by two elements and thus not regular.
is a height one local ring generated by two elements and thus not regular.
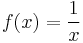
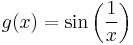
![\mathbb{C}[x,y] / (y^2 - x^3) \cong \mathbb{C}[t^2, t^3].](/2012-wikipedia_en_all_nopic_01_2012/I/425f87b0e4fa650700dc39017c5fdd15.png)