Matchstick graph

In geometric graph theory, a branch of mathematics, a matchstick graph is a graph that can be drawn in the plane in such a way that its edges are line segments with length one that do not cross each other. That is, it is a graph that has an embedding which is simultaneously a unit distance graph and a plane graph. Informally, matchstick graphs can be made by placing noncrossing matchsticks on a flat surface, hence the name.[1]

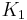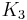It is known that there are matchstick graphs that are regular of any degree up to 4. The complete graphs K_1 and K_3 are 0-regular and 2-regular, respectively, and the path graph 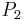P_2 is 1-regular. The smallest 3-regular matchstick graph is formed from two copies of the diamond graph placed in such a way that corresponding vertices are at unit distance from each other; its bipartite double cover is the 8-crossed prism graph.[1]

In 1986, Heiko Harborth presented the graph that would bear his name, the Harborth Graph. With 104 edges and 52 vertices, is the smallest known example of a 4-regular matchstick graph.[2] It is a rigid graph.[3]

There is a strong belief that there are no regular matchstick graphs of degree five, but the situation as of early 2010 seem to still be in flux with additional verification needed for the various proofs in circulation (cf. Blokhuis 2009, Kurz and Pinchasi 2009). [4] [5]

The smallest 3-regular matchstick graph without triangles (girth ≥ 4) has 20 vertices, as proved in 2009 by Kurz and Mazzuoccolo.[6] Furthermore, they exhibit the smallest known example of a 3-regular matchstick graph of girth 5 (180 vertices).

It is NP-hard to test whether a given undirected planar graph is a matchstick graph.[7][8]

References

  1. ^ a b Weisstein, Eric W., "Matchstick graph" from MathWorld.
  2. ^ Harborth, Heiko (1994), "Match sticks in the plane", in Guy, R. K.; Woodrow, R. E., The Lighter Side of Mathematics: Proceedings of the Eugéne Strens Memorial Conference of Recreational Mathematics and its History, Calgary, Canada, 1986, Washington, D.C.: Mathematical Association of America, pp. 281–288 . As cited in: Weisstein, Eric W., "Matchstick graph" from MathWorld.
  3. ^ Gerbracht, E. H.-A. (2006). "Minimal polynomials for the coordinates of the Harborth graph". arXiv:math.CO/0609360. . As cited in: Weisstein, Eric W., "Matchstick graph" from MathWorld.
  4. ^ Blokhuis, Aart (2009), Regular Finite Planar Maps with Equal Edges .
  5. ^ Kurz, S.; Pinchasi, R. (2009), Regular Matchstick Graphs, http://www.wm.uni-bayreuth.de/fileadmin/Sascha/Publikationen/regular_matchstick_graphs.pdf .
  6. ^ Kurz, Sascha; Mazzuoccolo, Giuseppe (2009), "3-regular matchstick graphs with given girth", Geombinatorics 19: 156–175 .
  7. ^ Eades, Peter; Wormald, Nicholas C. (1990), "Fixed edge-length graph drawing is NP-hard", Discrete Applied Mathematics 28 (2): 111–134, doi:10.1016/0166-218X(90)90110-X .
  8. ^ Cabello, Sergio; Demaine, Erik D.; Rote, Günter (2007), "Planar embeddings of graphs with specified edge lengths", Journal of Graph Algorithms and Applications 11 (1): 259–276, http://www.cs.brown.edu/sites/jgaa/accepted/2007/CabelloDemaineRote2007.11.1.pdf .