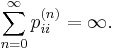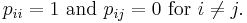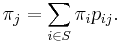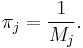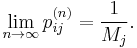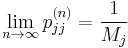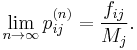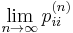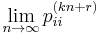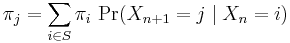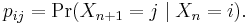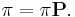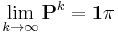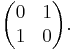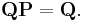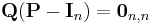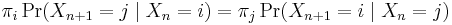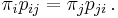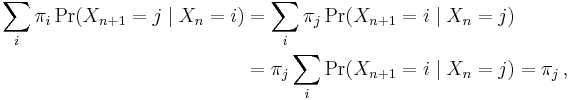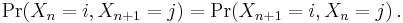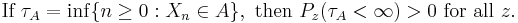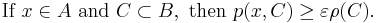Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the sequence of events that preceded it. This specific kind of "memorylessness" is called the Markov property. Markov chains have many applications as statistical models of real-world processes.
Contents |
Introduction
Formally, a Markov chain is a discrete (discrete-time) random process with the Markov property. Often, the term "Markov chain" is used to mean a Markov process which has a discrete (finite or countable) state-space. Usually a Markov chain is defined for a discrete set of times (i.e., a discrete-time Markov chain)[1] although some authors use the same terminology where "time" can take continuous values.[2][3] The use of the term in Markov chain Monte Carlo methodology covers cases where the process is in discrete time (discrete algorithm steps) with a continuous state space. The following concentrates on the discrete-time discrete-state-space case.
A discrete-time random process involves a system which is in a certain state at each step, with the state changing randomly between steps. The steps are often thought of as moments in time, but they can equally well refer to physical distance or any other discrete measurement; formally, the steps are the integers or natural numbers, and the random process is a mapping of these to states. The Markov property states that the conditional probability distribution for the system at the next step (and in fact at all future steps) depends only on the current state of the system, and not additionally on the state of the system at previous steps.
Since the system changes randomly, it is generally impossible to predict with certainty the state of a Markov chain at a given point in the future. However, the statistical properties of the system's future can be predicted. In many applications, it is these statistical properties that are important.
The changes of state of the system are called transitions, and the probabilities associated with various state-changes are called transition probabilities. The set of all states and transition probabilities completely characterizes a Markov chain. By convention, we assume all possible states and transitions have been included in the definition of the processes, so there is always a next state and the process goes on forever.
A famous Markov chain is the so-called "drunkard's walk", a random walk on the number line where, at each step, the position may change by +1 or −1 with equal probability. From any position there are two possible transitions, to the next or previous integer. The transition probabilities depend only on the current position, not on the manner in which the position was reached. For example, the transition probabilities from 5 to 4 and 5 to 6 are both 0.5, and all other transition probabilities from 5 are 0. These probabilities are independent of whether the system was previously in 4 or 6.
Another example is the dietary habits of a creature who eats only grapes, cheese or lettuce, and whose dietary habits conform to the following rules:
- It eats exactly once a day.
- If it ate cheese today, tomorrow it will eat lettuce or grapes with equal probability.
- If it ate grapes today, tomorrow it will eat grapes with probability 1/10, cheese with probability 4/10 and lettuce with probability 5/10.
- If it ate lettuce today, it will not eat lettuce again tomorrow but will eat grapes with probability 4/10 or cheese with probability 6/10.
This creature's eating habits can be modeled with a Markov chain since its choice tomorrow depends solely on what it ate today, not what it ate yesterday or even farther in the past. One statistical property that could be calculated is the expected percentage, over a long period, of the days on which the creature will eat grapes.
A series of independent events (for example, a series of coin flips) satisfies the formal definition of a Markov chain. However, the theory is usually applied only when the probability distribution of the next step depends non-trivially on the current state.
Many other examples of Markov chains exist.
Formal definition
A Markov chain is a sequence of random variables X1, X2, X3, ... with the Markov property, namely that, given the present state, the future and past states are independent. Formally,
The possible values of Xi form a countable set S called the state space of the chain.
Markov chains are often described by a directed graph, where the edges are labeled by the probabilities of going from one state to the other states.
Variations
- Continuous-time Markov processes have a continuous index.
- Time-homogeneous Markov chains (or stationary Markov chains) are processes where
- for all n. The probability of the transition is independent of n.
- A Markov chain of order m (or a Markov chain with memory m), where m is finite, is a process satisfying
- In other words, the future state depends on the past m states. It is possible to construct a chain (Yn) from (Xn) which has the 'classical' Markov property as follows:
- It can be proved that a Markov chain of order m can be in fact reduced to a Markov chain of order m = 1 (a simple Markov chain). Indeed, let Yn = (Xn, Xn−1, ..., Xn−m+1), the ordered m-tuple of X values. Then Yn is a Markov chain with state space Sm and has the classical Markov property.
- An additive Markov chain of order m is determined by an additive conditional probability,
The value f(xn,xn-r,r) is the additive contribution of the variable xn-r to the conditional probability.[4]
Example
A simple example is shown in the figure on the right, using a directed graph to picture the state transitions. The states represent whether the economy is in a bull market, a bear market, or a recession, during a given week. According to the figure, a bull week is followed by another bull week 90% of the time, a bear market 7.5% of the time, and a recession the other 2.5%. From this figure it is possible to calculate, for example, the long-term fraction of time during which the economy is in a recession, or on average how long it will take to go from a recession to a bull market.
A thorough development and many examples can be found in the on-line monograph Meyn & Tweedie 2005.[5] The appendix of Meyn 2007,[6] also available on-line, contains an abridged Meyn & Tweedie.
A finite state machine can be used as a representation of a Markov chain. Assuming a sequence of independent and identically distributed input signals (for example, symbols from a binary alphabet chosen by coin tosses), if the machine is in state y at time n, then the probability that it moves to state x at time n + 1 depends only on the current state.
Markov chains
The probability of going from state i to state j in n time steps is
and the single-step transition is
For a time-homogeneous Markov chain:
and
The n-step transition probabilities satisfy the Chapman–Kolmogorov equation, that for any k such that 0 < k < n,
where S is the state space of the Markov chain.
The marginal distribution Pr(Xn = x) is the distribution over states at time n. The initial distribution is Pr(X0 = x). The evolution of the process through one time step is described by
Note: The superscript (n) is an index and not an exponent.
Reducibility
A state j is said to be accessible from a state i (written i → j) if a system started in state i has a non-zero probability of transitioning into state j at some point. Formally, state j is accessible from state i if there exists an integer n ≥ 0 such that
Allowing n to be zero means that every state is defined to be accessible from itself.
A state i is said to communicate with state j (written i ↔ j) if both i → j and j → i. A set of states C is a communicating class if every pair of states in C communicates with each other, and no state in C communicates with any state not in C. It can be shown that communication in this sense is an equivalence relation and thus that communicating classes are the equivalence classes of this relation. A communicating class is closed if the probability of leaving the class is zero, namely that if i is in C but j is not, then j is not accessible from i.
That said, communicating classes need not be commutative, in that classes achieving greater periodic frequencies that encompass 100% of the phases of smaller periodic frequencies, may still be communicating classes provided a form of either diminished, downgraded, or multiplexed cooperation exists within the higher frequency class.
A state i is said to be essential if for all j such that i → j it is also true that j → i. A state i is inessential if it is not essential.[7]
Finally, a Markov chain is said to be irreducible if its state space is a single communicating class; in other words, if it is possible to get to any state from any state.
Periodicity
A state i has period k if any return to state i must occur in multiples of k time steps. Formally, the period of a state is defined as
(where "gcd" is the greatest common divisor). Note that even though a state has period k, it may not be possible to reach the state in k steps. For example, suppose it is possible to return to the state in {6, 8, 10, 12, ...} time steps; k would be 2, even though 2 does not appear in this list.
If k = 1, then the state is said to be aperiodic: returns to state i can occur at irregular times. Otherwise (k > 1), the state is said to be periodic with period k.
It can be shown that every state in a communicating class must have overlapping periods with all equivalent-or-larger occurring sample(s).
Every state of a bipartite graph has an even period.
Recurrence
A state i is said to be transient if, given that we start in state i, there is a non-zero probability that we will never return to i. Formally, let the random variable Ti be the first return time to state i (the "hitting time"):
The number
is the probability that we return to state i for the first time after n steps. Therefore, state i is transient if
State i is recurrent (or persistent) if it is not transient. Recurrent states have finite hitting time with probability 1.
Mean recurrence time
Even if the hitting time is finite with probability 1, it need not have a finite expectation. The mean recurrence time at state i is the expected return time Mi:
State i is positive recurrent (or non-null persistent) if Mi is finite; otherwise, state i is null recurrent (or null persistent).
Expected number of visits
It can be shown that a state i is recurrent if and only if the expected number of visits to this state is infinite, i.e.,
Absorbing states
A state i is called absorbing if it is impossible to leave this state. Therefore, the state i is absorbing if and only if
If every state can reach an absorbing state, then the Markov chain is an absorbing Markov chain.
Ergodicity
A state i is said to be ergodic if it is aperiodic and positive recurrent. If all states in an irreducible Markov chain are ergodic, then the chain is said to be ergodic.
It can be shown that a finite state irreducible Markov chain is ergodic if it has an aperiodic state. A model has the ergodic property if there's a finite number N such that any state can be reached from any other state in exactly N steps. In case of a fully connected transition matrix where all transitions have a non-zero probability, this condition is fulfilled with N=1. A model with more than one state and just one out-going transition per state cannot be ergodic.
Steady-state analysis and limiting distributions
If the Markov chain is a time-homogeneous Markov chain, so that the process is described by a single, time-independent matrix 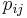 , then the vector
, then the vector 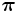 is called a stationary distribution (or invariant measure) if its entries
is called a stationary distribution (or invariant measure) if its entries 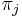 are non-negative and sum to 1 and if it satisfies
are non-negative and sum to 1 and if it satisfies
An irreducible chain has a stationary distribution if and only if all of its states are positive recurrent. In that case, π is unique and is related to the expected return time:
Further, if the chain is both irreducible and aperiodic, then for any i and j,
Note that there is no assumption on the starting distribution; the chain converges to the stationary distribution regardless of where it begins. Such π is called the equilibrium distribution of the chain.
If a chain has more than one closed communicating class, its stationary distributions will not be unique (consider any closed communicating class 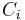 in the chain; each one will have its own unique stationary distribution
in the chain; each one will have its own unique stationary distribution 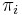 . Extending these distributions to the overall chain, setting all values to zero outside the communication class, yields that the set of invariant measures of the original chain is the set of all convex combinations of the
. Extending these distributions to the overall chain, setting all values to zero outside the communication class, yields that the set of invariant measures of the original chain is the set of all convex combinations of the 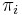 's). However, if a state j is aperiodic, then
's). However, if a state j is aperiodic, then
and for any other state i, let fij be the probability that the chain ever visits state j if it starts at i,
If a state i is periodic with period k > 1 then the limit
does not exist, although the limit
does exist for every integer r.
Steady-state analysis and the time-inhomogeneous Markov chain
A Markov chain need not necessarily be time-homogeneous to have an equilibrium distribution. If there is a probability distribution over states 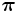 such that
such that
for every state j and every time n then 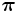 is an equilibrium distribution of the Markov chain. Such can occur in Markov chain Monte Carlo (MCMC) methods in situations where a number of different transition matrices are used, because each is efficient for a particular kind of mixing, but each matrix respects a shared equilibrium distribution.
is an equilibrium distribution of the Markov chain. Such can occur in Markov chain Monte Carlo (MCMC) methods in situations where a number of different transition matrices are used, because each is efficient for a particular kind of mixing, but each matrix respects a shared equilibrium distribution.
Finite state space
If the state space is finite, the transition probability distribution can be represented by a matrix, called the transition matrix, with the (i, j)th element of P equal to
Since each row of P sums to one and all elements are non-negative, P is a right stochastic matrix.
Time-homogeneous Markov chain with a finite state space
If the Markov chain is time-homogeneous, then the transition matrix P is the same after each step, so the k-step transition probability can be computed as the k-th power of the transition matrix, Pk.
The stationary distribution π is a (row) vector, whose entries are non-negative and sum to 1, that satisfies the equation
In other words, the stationary distribution π is a normalized (meaning that the sum of its entries is 1) left eigenvector of the transition matrix associated with the eigenvalue 1.
Alternatively, π can be viewed as a fixed point of the linear (hence continuous) transformation on the unit simplex associated to the matrix P. As any continuous transformation in the unit simplex has a fixed point, a stationary distribution always exists, but is not guaranteed to be unique, in general. However, if the Markov chain is irreducible and aperiodic, then there is a unique stationary distribution π. Additionally, in this case Pk converges to a rank-one matrix in which each row is the stationary distribution π, that is,
where 1 is the column vector with all entries equal to 1. This is stated by the Perron–Frobenius theorem. If, by whatever means, 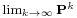 is found, then the stationary distribution of the Markov chain in question can be easily determined for any starting distribution, as will be explained below.
is found, then the stationary distribution of the Markov chain in question can be easily determined for any starting distribution, as will be explained below.
For some stochastic matrices P, the limit 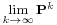 does not exist, as shown by this example:
does not exist, as shown by this example:
Because there are a number of different special cases to consider, the process of finding this limit if it exists can be a lengthy task. However, there are many techniques that can assist in finding this limit. Let P be an n×n matrix, and define 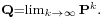
It is always true that
Subtracting Q from both sides and factoring then yields
where In is the identity matrix of size n, and 0n,n is the zero matrix of size n×n. Multiplying together stochastic matrices always yields another stochastic matrix, so Q must be a stochastic matrix. It is sometimes sufficient to use the matrix equation above and the fact that Q is a stochastic matrix to solve for Q. Including the fact that the sum of each the rows in P is 1, there are n+1 equations for determining n unknowns, so it is computationally easier if on the one hand one selects one row in Q and substitute each of its elements by one, and on the other one substitute the corresponding element (the one in the same column) in the vector 0, and next left-multiply this latter vector by the inverse of transformed former matrix to find Q.
Here is one method for doing so: first, define the function f(A) to return the matrix A with its right-most column replaced with all 1's. If [f(P − In)]−1 exists then
![\mathbf{Q}=f(\mathbf{0}_{n,n})[f(\mathbf{P}-\mathbf{I}_n)]^{-1}.](/2012-wikipedia_en_all_nopic_01_2012/I/d2409044bc560e731c8c1203f6c66062.png)
- Explain: The original matrix equation is equivalent to a system of n×n linear equations in n×n variables. And there are n more linear equations from the fact that Q is a right stochastic matrix whose each row sums to 1. So it needs any n×n independent linear equations of the (n×n+n) equations to solve for the n×n variables. In this example, the n equations from “Q multiplied by the right-most column of (P-In)” have been replaced by the n stochastic ones.
One thing to notice is that if P has an element Pi,i on its main diagonal that is equal to 1 and the ith row or column is otherwise filled with 0's, then that row or column will remain unchanged in all of the subsequent powers Pk. Hence, the ith row or column of Q will have the 1 and the 0's in the same positions as in P.
Reversible Markov chain
A Markov chain is said to be reversible if there is a probability distribution over states, π, such that
for all times n and all states i and j. This condition is also known as the detailed balance condition (some books refer the local balance equation). With a time-homogeneous Markov chain, Pr(Xn+1 = j | Xn = i) does not change with time n and it can be written more simply as 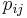 . In this case, the detailed balance equation can be written more compactly as
. In this case, the detailed balance equation can be written more compactly as
Summing the original equation over i gives
so, for reversible Markov chains, π is always a steady-state distribution of Pr(Xn+1 = j | Xn = i) for every n.
If the Markov chain begins in the steady-state distribution, i.e., if Pr(X0 = i) = πi, then Pr(Xn = i) = πi for all n and the detailed balance equation can be written as
The left- and right-hand sides of this last equation are identical except for a reversing of the time indices n and n + 1.
Reversible Markov chains are common in Markov chain Monte Carlo (MCMC) approaches because the detailed balance equation for a desired distribution π necessarily implies that the Markov chain has been constructed so that π is a steady-state distribution. Even with time-inhomogeneous Markov chains, where multiple transition matrices are used, if each such transition matrix exhibits detailed balance with the desired π distribution, this necessarily implies that π is a steady-state distribution of the Markov chain.
Bernoulli scheme
A Bernoulli scheme is a special case of a Markov chain where the transition probability matrix has identical rows, which means that the next state is even independent of the current state (in addition to being independent of the past states). A Bernoulli scheme with only two possible states is known as a Bernoulli process.
General state space
Many results for Markov chains with finite state space can be generalized to chains with uncountable state space through Harris chains. The main idea is to see if there is a point in the state space that the chain hits with probability one. Generally, it is not true for continuous state space, however, we can define sets A and B along with a positive number ε and a probability measure ρ, such that
Then we could collapse the sets into an auxiliary point α, and a recurrent Harris chain can be modified to contain α. Lastly, the collection of Harris chains is a comfortable level of generality, which is broad enough to contain a large number of interesting examples, yet restrictive enough to allow for a rich theory.
Applications
Markov chains are applied in a number of ways to many different fields. Often they are used as a mathematical model from some random physical process; if the parameters of the chain are known, quantitative predictions can be made. In other cases, they are used to model a more abstract process, and are the theoretical underpinning of an algorithm.
Physics
Markovian systems appear extensively in thermodynamics and statistical mechanics, whenever probabilities are used to represent unknown or unmodelled details of the system, if it can be assumed that the dynamics are time-invariant, and that no relevant history need be considered which is not already included in the state description.
Chemistry
Chemistry is often a place where Markov chains and continuous-time Markov processes are especially useful because these simple physical systems tend to satisfy the Markov property quite well. The classical model of enzyme activity, Michaelis-Menten kinetics, can be viewed as a Markov chain, where at each time step the reaction proceeds in some direction. While Michaelis-Menten is fairly straightforward, far more complicated reaction networks can also be modeled with Markov chains.
An algorithm based on a Markov chain was also used to focus the fragment-based growth of chemicals in silico towards a desired class of compounds such as drugs or natural products.[8] As a molecule is grown, a fragment is selected from the nascent molecule as the "current" state. It is not aware of its past (i.e., it is not aware of what is already bonded to it). It then transitions to the next state when a fragment is attached to it. The transition probabilities are trained on databases of authentic classes of compounds.
Also, the growth (and composition) of copolymers may be modeled using Markov chains. Based on the reactivity ratios of the monomers that make up the growing polymer chain, the chain's composition may be calculated (e.g., whether monomers tend to add in alternating fashion or in long runs of the same monomer). Due to steric effects, second-order Markov effects may also play a role in the growth of some polymer chains.
Testing
Several theorists have proposed the idea of the Markov chain statistical test (MCST), a method of conjoining Markov chains to form a "Markov blanket", arranging these chains in several recursive layers ("wafering") and producing more efficient test sets—samples—as a replacement for exhaustive testing. MCSTs also have uses in temporal state-based networks; Chilukuri et al.'s paper entitled "Temporal Uncertainty Reasoning Networks for Evidence Fusion with Applications to Object Detection and Tracking" (ScienceDirect) gives a background and case study for applying MCSTs to a wider range of applications.
Information sciences
Markov chains are used throughout information processing. Claude Shannon's famous 1948 paper A mathematical theory of communication, which in a single step created the field of information theory, opens by introducing the concept of entropy through Markov modeling of the English language. Such idealized models can capture many of the statistical regularities of systems. Even without describing the full structure of the system perfectly, such signal models can make possible very effective data compression through entropy encoding techniques such as arithmetic coding. They also allow effective state estimation and pattern recognition.
Markov chains are also the basis for Hidden Markov Models, which are an important tool in such diverse fields as telephone networks (for error correction), speech recognition and bioinformatics. The world's mobile telephone systems depend on the Viterbi algorithm for error-correction, while hidden Markov models are extensively used in speech recognition and also in bioinformatics, for instance for coding region/gene prediction. Markov chains also play an important role in reinforcement learning.
Queueing theory
Markov chains are the basis for the analytical treatment of queues (queueing theory). This makes them critical for optimizing the performance of telecommunications networks, where messages must often compete for limited resources (such as bandwidth).[6]
Internet applications
The PageRank of a webpage as used by Google is defined by a Markov chain.[9] It is the probability to be at page  in the stationary distribution on the following Markov chain on all (known) webpages. If
in the stationary distribution on the following Markov chain on all (known) webpages. If  is the number of known webpages, and a page
is the number of known webpages, and a page  has
has 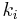 links then it has transition probability
links then it has transition probability 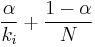 for all pages that are linked to and
for all pages that are linked to and 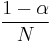 for all pages that are not linked to. The parameter
for all pages that are not linked to. The parameter  is taken to be about 0.85.[10]
is taken to be about 0.85.[10]
Markov models have also been used to analyze web navigation behavior of users. A user's web link transition on a particular website can be modeled using first- or second-order Markov models and can be used to make predictions regarding future navigation and to personalize the web page for an individual user.
Statistics
Markov chain methods have also become very important for generating sequences of random numbers to accurately reflect very complicated desired probability distributions, via a process called Markov chain Monte Carlo (MCMC). In recent years this has revolutionized the practicability of Bayesian inference methods, allowing a wide range of posterior distributions to be simulated and their parameters found numerically.
Economics and finance
Markov chains are used in Finance and Economics to model a variety of different phenomena, including asset prices and market crashes. The first financial model to use a Markov chain was from Prasad et al. in 1974.[11] Another was the regime-switching model of James D. Hamilton (1989), in which a Markov chain is used to model switches between periods of high volatility and low volatility of asset returns.[12] A more recent example is the Markov Switching Multifractal asset pricing model, which builds upon the convenience of earlier regime-switching models.[13] It uses an arbitrarily large Markov chain to drive the level of volatility of asset returns.
Dynamic macroeconomics heavily uses Markov chains. An example is using Markov chains to exogenously model prices of equity (stock) in a general equilibrium setting.[14]
Leontief's Input-output model is a Markov chain.
Social sciences
Markov chains are generally used in describing path-dependent arguments, where current structural configurations condition future outcomes. An example is the commonly argued link between economic development and the rise of capitalism. Once a country reaches a specific level of economic development, the configuration of structural factors, such as size of the commercial bourgeoisie, the ratio of urban to rural residence, the rate of political mobilization, etc., will generate a higher probability of transitioning from authoritarian to capitalist.
Mathematical biology
Markov chains also have many applications in biological modelling, particularly population processes, which are useful in modelling processes that are (at least) analogous to biological populations. The Leslie matrix is one such example, though some of its entries are not probabilities (they may be greater than 1). Another example is the modeling of cell shape in dividing sheets of epithelial cells.[15] Yet another example is the state of Ion channels in cell membranes.
Markov chains are also used in simulations of brain function, such as the simulation of the mammalian neocortex.[16]
Games
Markov chains can be used to model many games of chance. The children's games Snakes and Ladders and "Hi Ho! Cherry-O", for example, are represented exactly by Markov chains. At each turn, the player starts in a given state (on a given square) and from there has fixed odds of moving to certain other states (squares).
Music
Markov chains are employed in algorithmic music composition, particularly in software programs such as CSound, Max or SuperCollider. In a first-order chain, the states of the system become note or pitch values, and a probability vector for each note is constructed, completing a transition probability matrix (see below). An algorithm is constructed to produce and output note values based on the transition matrix weightings, which could be MIDI note values, frequency (Hz), or any other desirable metric.[17]
| Note | A | C♯ | E♭ |
|---|---|---|---|
| A | 0.1 | 0.6 | 0.3 |
| C♯ | 0.25 | 0.05 | 0.7 |
| E♭ | 0.7 | 0.3 | 0 |
| Note | A | D | G |
|---|---|---|---|
| AA | 0.18 | 0.6 | 0.22 |
| AD | 0.5 | 0.5 | 0 |
| AG | 0.15 | 0.75 | 0.1 |
| DD | 0 | 0 | 1 |
| DA | 0.25 | 0 | 0.75 |
| DG | 0.9 | 0.1 | 0 |
| GG | 0.4 | 0.4 | 0.2 |
| GA | 0.5 | 0.25 | 0.25 |
| GD | 1 | 0 | 0 |
A second-order Markov chain can be introduced by considering the current state and also the previous state, as indicated in the second table. Higher, nth-order chains tend to "group" particular notes together, while 'breaking off' into other patterns and sequences occasionally. These higher-order chains tend to generate results with a sense of phrasal structure, rather than the 'aimless wandering' produced by a first-order system.[18]
Markov chains can be used structurally, as in Xenakis's Analogique A and B, as described in his book 'Formalized Music: Mathematics and Thought in Composition'. Markov chains are also used in systems such as the Continuator and the Virtuoso, which use a Markov model to react interactively to music input.
It should be noted that usually musical systems need to enforce specific control constraints on the finite-length sequences they generate, but control constraints are not compatible with Markov models, since they induce long-range dependencies that violate the Markov hypothesis of limited memory. In order to overcome this limitation, a new approach has been proposed by Pachet and Roy. [19]
Baseball
Markov chain models have been used in advanced baseball analysis since 1960, although their use is still rare. Each half-inning of a baseball game fits the Markov chain state when the number of runners and outs are considered. During any at-bat, there are 24 possible combinations of number of outs and position of the runners. Mark Pankin shows that Markov chain models can be used to evaluate runs created for both individual players as well as a team.[20] He also discusses various kinds of strategies and play conditions: how Markov chain models have been used to analyze statistics for game situations such as bunting and base stealing and differences when playing on grass vs. astroturf.[21]
Markov text generators
Markov processes can also be used to generate superficially "real-looking" text given a sample document: they are used in a variety of recreational "parody generator" software (see dissociated press, Jeff Harrison [1], Mark V Shaney[22][23] ).
These processes are also used by spammers to inject real-looking hidden paragraphs into unsolicited email in an attempt to get these messages past spam filters.
Fitting
When fitting a Markov chain to data, situations where parameters poorly describe the situation may highlight interesting trends.[24]
History
Andrey Markov produced the first results (1906) for these processes, purely theoretically. A generalization to countably infinite state spaces was given by Kolmogorov (1936). Markov chains are related to Brownian motion and the ergodic hypothesis, two topics in physics which were important in the early years of the twentieth century, but Markov appears to have pursued this out of a mathematical motivation, namely the extension of the law of large numbers to dependent events. In 1913, he applied his findings for the first time to the first 20,000 letters of Pushkin's Eugene Onegin.
Seneta provides an account of Markov's motivations and the theory's early development.[25] The term "chain" was used by Markov (1906).[26]
See also
Notes
- ^ Everitt,B.S. (2002) The Cambridge Dictionary of Statistics. CUP. ISBN 0-521-81099-x
- ^ Parzen, E. (1962) Stochastic Processes, Holden-Day. ISBN 0-8162-6664-6 (Table 6.1))
- ^ Dodge, Y. (2003) The Oxford Dictionary of Statistical Terms, OUP. ISBN 0-19-920613-9 (entry for "Markov chain")
- ^ Usatenko, O. V.; Apostolov, S. S.; Mayzelis, Z. A.; Melnik, S. S. (2010) Random finite-valued dynamical systems: additive Markov chain approach. Cambridge Scientific Publisher. ISBN 978-1-904868-74-3
- ^ S. P. Meyn and R.L. Tweedie, 2005. Markov Chains and Stochastic Stability. Second edition to appear, Cambridge University Press, 2008.
- ^ a b S. P. Meyn, 2007. Control Techniques for Complex Networks, Cambridge University Press, 2007.
- ^ Asher Levin, David (2009). Markov chains and mixing times. pp. 16. ISBN 9780821847398. http://books.google.co.uk/books?id=6Cg5Nq5sSv4C&lpg=PA16&dq=essential%20class%20markov&pg=PA16#v=onepage.
- ^ Kutchukian, Peter; Lou, David; Shakhnovich, Eugene (2009). "FOG: Fragment Optimized Growth Algorithm for the de Novo Generation of Molecules occupying Druglike Chemical". Journal of Chemical Information and Modeling 49 (7): 1630–1642. doi:10.1021/ci9000458. PMID 19527020.
- ^ U.S. Patent 6,285,999
- ^ Page, Lawrence and Brin, Sergey and Motwani, Rajeev and Winograd, Terry (1999). The PageRank Citation Ranking: Bringing Order to the Web (Technical report). http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.31.1768.
- ^ Prasad, NR; RC Ender,ST Reilly,G Nesgos (1974). "Allocation of resources on a minimized cost basis". 1974 IEEE Conference on Decision and Control including the 13th Symposium on Adaptive Processes 13: 402–3. doi:10.1109/CDC.1974.270470. http://ieeexplore.ieee.org/Xplore/defdeny.jsp?url=http://ieeexplore.ieee.org/stamp/stamp.jsp%3Ftp%3D%26arnumber%3D4045263%26userType%3Dinst&denyReason=-133&arnumber=4045263&productsMatched=null&userType=inst.
- ^ Hamilton, James (1989). "A new approach to the economic analysis of nonstationary time series and the business cycle". Econometrica (Econometrica, Vol. 57, No. 2) 57 (2): 357–84. doi:10.2307/1912559. JSTOR 1912559.
- ^ Calvet, Laurent; Adlai Fisher (2004). "How to Forecast long-run volatility: regime-switching and the estimation of multifractal processes". Journal of Financial Econometrics 2: 49–83. doi:10.1093/jjfinec/nbh003.
- ^ Brennan, Michael; Xiab, Yihong. "Stock Price Volatility and the Equity Premium". Department of Finance, the Anderson School of Management, UCLA. http://bbs.cenet.org.cn/uploadImages/200352118122167693.pdf.
- ^ Emergence of geometric order in proliferating metazoan epithelia by Ankit B. Patel, Radhika Nagpal
- ^ George, Dileep; Hawkins, Jeff (2009). Friston, Karl J.. ed. "Towards a Mathematical Theory of Cortical Micro-circuits". PLoS Comput Biol 5 (10): e1000532. doi:10.1371/journal.pcbi.1000532. PMC 2749218. PMID 19816557. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2749218.
- ^ K McAlpine, E Miranda, S Hoggar (1999). "Making Music with Algorithms: A Case-Study System". Computer Music Journal 23 (2): 19. doi:10.1162/014892699559733. http://www.mitpressjournals.org/doi/abs/10.1162/014892699559733.
- ^ Curtis Roads (ed.) (1996). The Computer Music Tutorial. MIT Press. ISBN 0262181584.
- ^ Pachet, F., Roy, P. and Barbieri, G. Finite-Length Markov Processes with Constraints, Proceedings of the 22nd International Joint Conference on Artificial Intelligence, IJCAI, pages 635-642,Barcelona, Spain, July 2011
- ^ Pankin, Mark D.. "MARKOV CHAIN MODELS: THEORETICAL BACKGROUND". http://www.pankin.com/markov/theory.htm. Retrieved 2007-11-26.
- ^ Pankin, Mark D.. "BASEBALL AS A MARKOV CHAIN". http://www.pankin.com/markov/intro.htm. Retrieved 2009-04-24.
- ^ Kenner, Hugh; O'Rourke, Joseph (November 1984). "A Travesty Generator for Micros". BYTE 9 (12): 129–131, 449–469
- ^ Hartman, Charles (1996). The Virtual Muse: Experiments in Computer Poetry. Hanover, NH: Wesleyan University Press. ISBN 0819522392
- ^ Avery, P. J.; Henderson, D. A. (1999). "Fitting Markov Chain Models to Discrete State Series Such as DNA Sequences". Journal of the Royal Statistical Society 48 (1): 53–61. doi:10.1111/1467-9876.00139. JSTOR 2680818.
- ^ Seneta, E. (1996). "Markov and the Birth of Chain Dependence Theory". International Statistical Review 64 (3): 255–263. doi:10.2307/1403785. JSTOR 1403785.
- ^ Upton, G.; Cook, I. (2008). Oxford Dictionary of Statistics. OUP. ISBN 0199541454.
References
- A.A. Markov. "Rasprostranenie zakona bol'shih chisel na velichiny, zavisyaschie drug ot druga". Izvestiya Fiziko-matematicheskogo obschestva pri Kazanskom universitete, 2-ya seriya, tom 15, pp. 135–156, 1906.
- A.A. Markov. "Extension of the limit theorems of probability theory to a sum of variables connected in a chain". reprinted in Appendix B of: R. Howard. Dynamic Probabilistic Systems, volume 1: Markov Chains. John Wiley and Sons, 1971.
- Classical Text in Translation: A. A. Markov, An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains, trans. David Link. Science in Context 19.4 (2006): 591–600. Online: http://journals.cambridge.org/production/action/cjoGetFulltext?fulltextid=637500
- Leo Breiman. Probability. Original edition published by Addison-Wesley, 1968; reprinted by Society for Industrial and Applied Mathematics, 1992. ISBN 0-89871-296-3. (See Chapter 7.)
- J.L. Doob. Stochastic Processes. New York: John Wiley and Sons, 1953. ISBN 0-471-52369-0.
- S. P. Meyn and R. L. Tweedie. Markov Chains and Stochastic Stability. London: Springer-Verlag, 1993. ISBN 0-387-19832-6. online: https://netfiles.uiuc.edu/meyn/www/spm_files/book.html . Second edition to appear, Cambridge University Press, 2009.
- S. P. Meyn. Control Techniques for Complex Networks. Cambridge University Press, 2007. ISBN 978-0-521-88441-9. Appendix contains abridged Meyn & Tweedie. online: https://netfiles.uiuc.edu/meyn/www/spm_files/CTCN/CTCN.html
- Booth, Taylor L. (1967). Sequential Machines and Automata Theory (1st ed.). New York: John Wiley and Sons, Inc.. Library of Congress Card Catalog Number 67-25924. Extensive, wide-ranging book meant for specialists, written for both theoretical computer scientists as well as electrical engineers. With detailed explanations of state minimization techniques, FSMs, Turing machines, Markov processes, and undecidability. Excellent treatment of Markov processes pp. 449ff. Discusses Z-transforms, D transforms in their context.
- Kemeny, John G.; Hazleton Mirkil, J. Laurie Snell, Gerald L. Thompson (1959). Finite Mathematical Structures (1st ed.). Englewood Cliffs, N.J.: Prentice-Hall, Inc.. Library of Congress Card Catalog Number 59-12841. Classical text. cf Chapter 6 Finite Markov Chains pp. 384ff.
- E. Nummelin. "General irreducible Markov chains and non-negative operators". Cambridge University Press, 1984, 2004. ISBN 0-521-60494-X
- Seneta, E. Non-negative matrices and Markov chains. 2nd rev. ed., 1981, XVI, 288 p., Softcover Springer Series in Statistics. (Originally published by Allen & Unwin Ltd., London, 1973) ISBN 978-0-387-29765-1
- Kishor S. Trivedi, Probability and Statistics with Reliability, Queueing, and Computer Science Applications, John Wiley & Sons, Inc. New York, 2002. ISBN 0-471-33341-7.
- K.S.Trivedi and R.A.Sahner, SHARPE at the age of twenty-two, vol. 36, no. 4, pp.-52-57, ACM SIGMETRICS Performance Evaluation Review, 2009.
- R.A.Sahner, K.S.Trivedi and A. Puliafito, Performance and reliability analysis of computer systems: an example-based approach using the SHARPE software package, Kluwer Academic Publishers, 1996. ISBN 0-7923-9650-2.
- G.Bolch, S.Greiner, H.de Meer and K.S.Trivedi, Queueing Networks and Markov Chains, John Wiley, 2nd edition, 2006. ISBN 9780792396505.
External links
- Techniques to Understand Computer Simulations: Markov Chain Analysis
- Markov Chains chapter in American Mathematical Society's introductory probability book(pdf)
- Markov Chains
- Class structure on PlanetMath
- Chapter 5: Markov Chain Models
- A JavaScript Markovian text compressor (in Portuguese).
- Application to Markov Chains
- Generating Text:Section 15.3 of Programming Pearls
- Generating Text Online: Markov Random Walk v1.1
- a list of recourses related to Markov chains
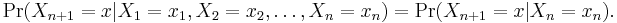

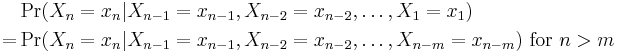
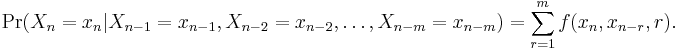
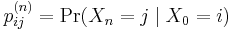
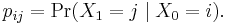
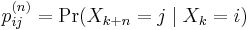
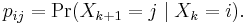
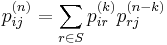
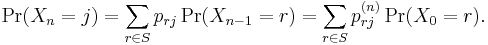
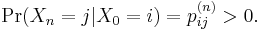
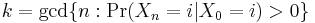
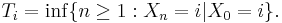
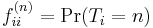
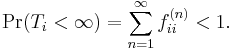
![M_i = E[T_i]=\sum_{n=1}^{\infty} n\cdot f_{ii}^{(n)}.\,](/2012-wikipedia_en_all_nopic_01_2012/I/8d156b3d9cdef4da6d8413d5fce3408e.png)