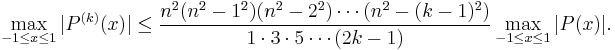Markov brothers' inequality
In mathematics, the Markov brothers' inequality is an inequality proved by Andrey Markov and Vladimir Markov. This inequality bounds the maximum of the derivatives of a polynomial on an interval in terms of the maximum of the polynomial.[1] For k = 1 it was proved by Andrey Markov,[2] and for k = 2,3,... by his brother Vladimir Markov.[3]
The statement
Let P be a polynomial of degree ≤ n. Then
Equality is attained for Chebyshev polynomials of the first kind.
Related inequalities
References
- ^ Achiezer, N.I. (1992). Theory of approximation. New York: Dover Publications, Inc..
- ^ Markov, A.A. (1890). "On a question by D. I. Mendeleev". Zap. Imp. Akad. Nauk SPb. 62: 1–24.
- ^ Markov, V.A. (1892). О функциях, наименее уклоняющихся от нуля в данном промежутке (On Functions of Least Deviation from Zero in a Given Interval). Appeared in German with a foreword by Sergei Bernstein as Markov, V.A. (1916). "Über Polynome, die in einem gegebenen Intervalle möglichst wenig von Null abweichen". Math. Ann. 77: 213–258.