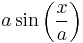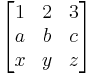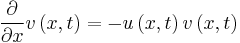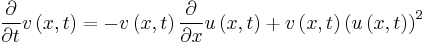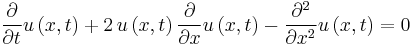Maple (software)

Maple
Maple interface
Developer(s)	Waterloo Maple (Maplesoft)
Stable release	15.01 / June 21, 2011; 7 months ago (2011-06-21)
Type	Computer algebra system
License	Proprietary commercial software
Website	www.maplesoft.com/products/maple/

Maple is a general-purpose commercial computer algebra system. It was first developed in 1980 by the Symbolic Computation Group at the University of Waterloo in Waterloo, Ontario, Canada.

Since 1988, it has been developed and sold commercially by Waterloo Maple Inc. (also known as Maplesoft), a Canadian company also based in Waterloo, Ontario. The current major version is version 15 which was released in April 2011.

Overview

Core functionality

Users can enter mathematics in traditional mathematical notation. Custom user interfaces can also be created. There is extensive support for numeric computations, to arbitrary precision, as well as symbolic computation and visualization. Examples of symbolic computations are given below.

Maple incorporates a dynamically typed imperative-style programming language which resembles Pascal.^[1] The language permits variables of lexical scope. There are also interfaces to other languages (C, C#, Fortran, Java, MATLAB, and Visual Basic). There is also an interface with Excel.

Maple supports MathML 2.0, a W3C format for representing and interpreting mathematical expressions, including their display in Web pages.^[2]

Architecture

Maple is based on a small kernel, written in C, which provides the Maple language. Most functionality is provided by libraries, which come from a variety of sources. Many numerical computations are performed by the NAG Numerical Libraries, ATLAS libraries, or GMP libraries. Most of the libraries are written in the Maple language; these have viewable source code.

Different functionality in Maple requires numerical data in different formats. Symbolic expressions are stored in memory as directed acyclic graphs. The standard interface and calculator interface are written in Java. The classic interface is written in C.

Examples of Maple code

Sample imperative programming constructs:

myfac := proc(n::nonnegint)
   local out, i;
   out := 1;
   for i from 2 to n do
       out := out * i
   end do;
   out
end proc;

Simple functions can also be defined using the "maps to" arrow notation:

myfac := n -> product( i, i=1..n );

Integration

Find

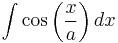$\int\cos\left(\frac{x}{a}\right)dx$ .

int(cos(x/a), x);

Answer:

$a \sin\left(\frac{x}{a}\right)$

Solution of linear differential equations

Compute an exact solution to the linear ordinary differential equation 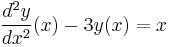$\frac{d^2y}{dx^2}(x) - 3 y(x) = x$ subject to initial conditions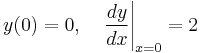 $y(0) = 0 ,\quad \left. \frac{dy}{dx} \right|_{x=0} = 2$

dsolve( {diff(y(x),x,x) - 3*y(x) = x, y(0)=0, D(y)(0)=2}, y(x) );

Answer: 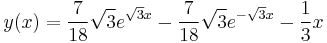$y(x)=\frac{7}{18}\sqrt{3}e^{\sqrt{3}x}-\frac{7}{18}\sqrt{3}e^{-\sqrt{3}x}-\frac{1}{3}x$

Root finding

Numerically calculate the root of the equation 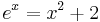$e^x=x^2%2B2\,\!$ starting at the point 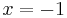$x=-1\,\!$ ; evaluate the answer to 75 decimal digits.

evalf[75](RootOf(exp(x)=x^2+2,x,-1));

Answer: 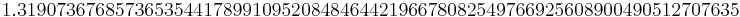$1.31907367685736535441789910952084846442196678082549766925608900490512707635$

Solving equations and inequalities

Find all solutions of 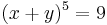$(x%2By)^5 = 9$ subject to $x-y > 6$ .

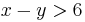solve({x-y > 6, (x+y)^5 = 9}, [x, y])[];

Answer: $[x = 3^{2/5}-y, \quad y < \frac{1}{2}3^{2/5}-3]$

Determinant

Compute the determinant of a matrix.

M:= Matrix([[1,2,3], [a,b,c], [x,y,z]]);  # example Matrix

$\begin{bmatrix} 1 & 2 & 3 \\ a & b & c \\ x & y & z \end{bmatrix}$

LinearAlgebra:-Determinant(M);

Answer: 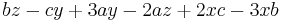$bz-cy%2B3ay-2az%2B2xc-3xb$

Plotting of function of single variable

Plot 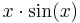$x \cdot \sin(x)$ with $x$ ranging from -10 to 10

plot(x*sin(x),x=-10..10);

Plotting of function of two variables

Plot 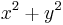$x^2%2By^2$ with $x$ and $y$ ranging from -1 to 1

plot3d(x^2+y^2,x=-1..1,y=-1..1);

System of partial differential equations

Solve the system of partial differential equations

${\frac {\partial }{\partial x}}v \left( x,t \right) =-u \left( x,t \right) v \left( x,t \right)$

${\frac {\partial }{\partial t}}v \left( x,t \right) =-v \left( x,t \right) {\frac {\partial }{\partial x}}u \left( x,t \right) %2Bv \left( x,t \right) \left( u \left( x,t \right) \right) ^{2}$

${\frac {\partial }{\partial t}}u \left( x,t \right) %2B2\,u \left( x,t \right) {\frac {\partial }{ \partial x}}u \left( x,t \right) -{\frac {\partial ^{2}}{\partial {x}^{2}}}u \left( x,t \right) =0$

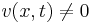with $v(x,t)\neq 0$ .

eqn1:= diff(v(x, t), x) = -u(x,t)*v(x,t):
eqn2:= diff(v(x, t), t) = -v(x,t)*(diff(u(x,t), x))+v(x,t)*u(x,t)^2:
eqn3:= diff(u(x,t), t)+2*u(x,t)*(diff(u(x,t), x))-(diff(diff(u(x,t), x), x)) = 0:
pdsolve({eqn1,eqn2,eqn3,v(x,t)<>0},[u,v]): op(%);

Answer: 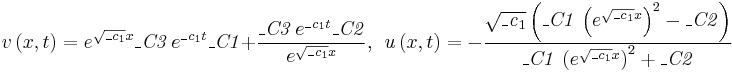$v \left( x,t \right) ={e^{\sqrt {{\it \_c}_{{1}}}x}}{\it \_C3 }\,{e^{{\it \_c}_{{1}}t}}{\it \_C1}%2B{\frac {{\it \_C3}\,{e^{{\it \_c}_ {{1}}t}}{\it \_C2}}{{e^{\sqrt {{\it \_c}_{{1}}}x}}}}, \ \ u \left( x,t \right) =-{\frac {\sqrt {{\it \_c}_{{1}}} \left( {\it \_C1}\, \left( {e^{\sqrt {{\it \_c}_{{1}}}x}} \right) ^{2}-{\it \_C2} \right) }{{\it \_C1}\, \left( {e^{\sqrt {{\it \_c}_{{1}}}x}} \right) ^{2}%2B{\it \_C2}} }$

Integral equations

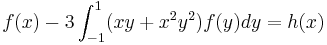Find functions $f$ that satisfy the integral equation $f(x)-3\int_{-1}^1(xy%2Bx^2y^2)f(y)dy = h(x)$ .

eqn:= f(x)-3*Integrate((x*y+x^2*y^2)*f(y), y=-1..1) = h(x):
intsolve(eqn,f(x));

Answer: 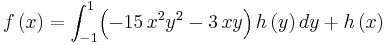$f \left( x \right) =\int _{-1}^{1}\! \left( -15\,{x}^{2}{y}^{2}-3\,xy \right) h \left( y \right) {dy}%2Bh \left( x \right)$

History

The first concept of Maple arose from a meeting in November 1980 at the University of Waterloo. Researchers at the university wished to purchase a computer powerful enough to run Macsyma. Instead, it was decided that they would develop their own computer algebra system that would be able to run on more reasonably priced computers. The first limited version appearing in December 1980 with Maple demonstrated first at conferences beginning in 1982. The name is a reference to Maple's Canadian heritage. By the end of 1983, over 50 universities had copies of Maple installed on their machines.

In 1984, the research group arranged with Watcom Products Inc to license and distribute Maple. In 1988 Waterloo Maple Inc. was founded. The company’s original goal was to manage the distribution of the software. Eventually, the company evolved to have an R&D department where much of Maple's development is done today, but significant development of Maple continues at university research labs including: the Symbolic Computation Laboratory at the University of Waterloo; the Ontario Research Centre for Computer Algebra at the University of Western Ontario; and labs at other universities worldwide.

In 1989, the first graphical user interface for Maple was developed and included with version 4.3 for the Macintosh. X11 and Windows versions of the new interface followed in 1990 with Maple V. Maple was used in a number of notable applications in science and mathematics ranging from a demonstration of Fermat's Last Theorem in number theory, to solutions in General Relativity and quantum mechanics. These were showcased in a special issue of a newsletter created by Maple developers called MapleTech'.^[3]

In 1999, with the release of Maple 6, Maple included some of the NAG Numerical Libraries,^[4] and made improvements to arbitrary precision arithmetic.

In 2003, the current "standard" interface was introduced with Maple 9. This interface is primarily written in Java (although portions, such as the rules for typesetting mathematical formulae, are written in the Maple language). The Java interface was criticized for being slow;^[5] improvements have been made in later versions, although the Maple 11 documentation^[6] recommends the previous (“classic”) interface for users with less than 500 MB of physical memory. This classic interface is no longer being maintained.

Between the mid 1995 and 2005 Maple lost significant market share to competitors due to a weaker user interface.^[7] In 2005, Maple 10 introduced a new “document mode”, as part of the standard interface. The main feature of this mode is that math is entered using two dimensional input, so that it appears similar to formulae in a book. In 2008, Maple 12 added additional user interface features found in Mathematica, including special purpose style sheets, control of headers and footers, bracket matching, auto execution regions, command completion templates, syntax checking and auto-initialization regions. Additional features were added for making Maple easier to use as a MATLAB toolbox.^[8]

In September 2009 Maple and Maplesoft were acquired by the Japanese software retailer Cybernet Systems.

Releases

Maple 1.0: January, 1982
Maple 1.1: January, 1982
Maple 2.0: May, 1982
Maple 2.1: June, 1982
Maple 2.15: August, 1982
Maple 2.2: December, 1982
Maple 3.0: May, 1983
Maple 3.1: October, 1983
Maple 3.2: April, 1984
Maple 3.3: March, 1985 (first public available version)
Maple 4.0: April, 1986
Maple 4.1: May, 1987
Maple 4.2: December, 1987
Maple 4.3: March, 1989
Maple V: August, 1990
Maple V R2: November 1992
Maple V R3: March 15, 1994
Maple V R4: January, 1996
Maple V R5: November 1, 1997
Maple 6: December 6, 1999
Maple 7: July 1, 2001
Maple 8: April 16, 2002
Maple 9: June 30, 2003
Maple 9.5: April 15, 2004
Maple 10: May 10, 2005
Maple 11: February 21, 2007
Maple 12: May, 2008
Maple 13: April, 2009
Maple 14: April 2010
Maple 14.01: October 28, 2010
Maple 15: April 13, 2011
Maple 15.01: June 21, 2011

Use of the Maple engine

The Maple engine is used within several other products from Maplesoft:

Maple T.A., Maplesoft’s online testing suite, uses Maple to algorithmically generate questions and grade student responses.
MapleNet allows users to create JSP pages and Java Applets. MapleNet 12 and above also allow users to upload and work with Maple worksheets containing interactive components.
Maple Reader, Maplesoft’s platform for DRM-controlled electronic books uses the Standard Maple interface. There are currently no available books using this product.
MapleSim, an engineering simulation tool.

Listed below are third-party commercial products that no longer use the Maple engine:

Versions of MathCad released between 1994 and 2006 included a Maple-derived algebra engine (MKM, aka Mathsoft Kernel Maple), though subsequent versions use MuPAD.
Symbolic Math Toolbox in MATLAB contained a portion of the Maple 10 engine but now uses MuPAD.
Older versions of the mathematical editor Scientific Workplace included Maple as a computational engine, though current versions include MuPAD.

Versions available

Maplesoft sells student, personal, academic and professional editions of Maple, with a substantial difference in price (US$99, $239cdn, US$1245, and US$2,275, respectively). Later student editions (from version 6 onwards) have not placed computational limitations, but rather come with less printed documentation when purchased as a physical product. There is no difference in the product when purchased as an electronic download. Since Maple 14, all versions include the Maple Toolbox for MATLAB, which used to be available as a separate product available only for academic and professional users.^[9]

Copy protection

Single-user editions of Maple are locked to the hardware of the computer they run on. This means that Maple may refuse to start if certain parts of the computer's hardware are removed or replaced. In this case the customer support has to be called to receive a new licence file for the updated hardware.

References

^ Power of two Bitwise Magazine
^ http://www.maplesoft.com/standards/MathML/info.html
^ MapleTech Special Issue, Birkhäuser-Boston, (1994)
^ Maple 6.0 Macworld, Feb 2001
^ Capturing knowledge with pure maths, Scientific Computing World.
^ Maple 11 Installation Guide
^ Interview with Gaston Gonnet, co-creator of Maple, SIAM History of Numerical Analysis and Computing, March 16, 2005
^ New in Maple 12 Maplesoft
^ Advanced technology for design, modeling and high-performance simulation saves engineers time and effort

External links

Maplesoft, division of Waterloo Maple, Inc. home website
MaplePrimes - a community website for Maple users
Comparison of mathematical programs for data analysis ScientificWeb

Computer algebra systems

Retail	Algebrator · ClassPad Manager · LiveMath · Magma · Maple · Mathcad · Mathematica · MuPAD (MATLAB symbolic math toolbox) · TI InterActive! · WIRIS

Open source	Axiom · Cadabra · CoCoA · DoCon · Eigenmath · FriCAS · GAP · GiNaC · Macaulay2 · Mathomatic · Maxima · OpenAxiom · PARI/GP · Reduce · Sage · SINGULAR · SymPy · Xcas · Yacas

Free/shareware	Fermat

Discontinued	Derive · DCAS · Macsyma · muMATH

Category • Comparison

Numerical software

Free Software	ADMB Euler FreeMat Genius GNU Octave gretl R Sage Scilab

Proprietary	DADiSP GAUSS LabVIEW MATLAB Mathematica Speakeasy VisSim

List of numerical analysis software Comparison of numerical analysis software