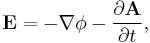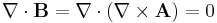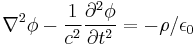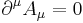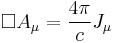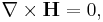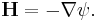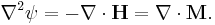Magnetic potential

Electromagnetism

Electricity Magnetism
Electrostatics Electric charge Coulomb's law Electric field Electric flux Gauss's law Electric potential energy Electric potential Electrostatic induction Electric dipole moment Polarization density
Magnetostatics Ampère's law Electric current Magnetic field Magnetization Magnetic flux Biot–Savart law Magnetic dipole moment Gauss's law for magnetism
Electrodynamics Lorentz force law emf Electromagnetic induction Faraday’s law Lenz's law Displacement current Maxwell's equations EM field Electromagnetic radiation Liénard–Wiechert potential Maxwell tensor Eddy current
Electrical Network Electrical conduction Electrical resistance Capacitance Inductance Impedance Resonant cavities Waveguides
Covariant formulation Electromagnetic tensor EM Stress-energy tensor Four-current Electromagnetic four-potential
Scientists Ampère Coulomb Faraday Gauss Heaviside Henry Hertz Lorentz Maxwell Tesla Volta Weber Ørsted

The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, (often simply called the vector potential) and the magnetic scalar potential, ψ. Both quantities can be used in certain circumstances to calculate the magnetic field.

The more frequently used magnetic vector potential A (often simply called the vector potential) is defined such that the curl of A is the magnetic B field. Together with the electric potential, the magnetic vector potential can be used to specify the electric field, E as well. Therefore, many equations of electromagnetism can be written either in terms of the E and B, or in terms of the magnetic vector potential and electric potential. In more advanced theories such as quantum mechanics, most equations use the potentials and not the E and B fields.

The magnetic scalar potential ψ is sometimes used to specify the magnetic H-field in cases when there are no free currents, in a manner analogous to using the electric potential to determine the electric field in electrostatics. One important use of ψ is to determine the magnetic field due to permanent magnets when their magnetization is known. With some care the scalar potential can be extended to include free currents as well.

1 Magnetic vector potential
2 Magnetic scalar potential
3 Notes
4 References

Magnetic vector potential

The magnetic vector potential A is a vector field that together with the (scalar field) electric potential φ are defined as:

$\mathbf{B} = \nabla \times \mathbf{A},$ ^[1]

$\mathbf{E} = - \nabla \phi - \frac { \partial \mathbf{A} } { \partial t },$ ^[1]

where B is the magnetic field and E is the electric field. In magnetostatics where there is no time varying charge distribution, only the first equation is needed. (In the context of electrodynamics, the terms "vector potential" and "scalar potential" are used for "magnetic vector potential" and "electric potential", respectively. In mathematics, vector potential and scalar potential have more general meanings.)

Defining the electric and magnetic fields from potentials automatically satisfies two of Maxwell's equations: Gauss's law for magnetism and Faraday's Law. For example, if A is continuous and well-defined everywhere, then it is guaranteed not to result in magnetic monopoles. (In the mathematical theory of magnetic monopoles, A is allowed to be either undefined or multiple-valued in some places; see magnetic monopole for details.)

Starting with the above definitions:

$\nabla \cdot \mathbf{B} = \nabla \cdot (\nabla \times \mathbf{A}) = 0$

$\nabla \times \mathbf{E} = \nabla \times \left( - \nabla \phi - \frac { \partial \mathbf{A} } { \partial t } \right) = - \frac { \partial } { \partial t } (\nabla \times \mathbf{A}) = - \frac { \partial \mathbf{B} } { \partial t }.$

Alternatively, the existence of A and φ is guaranteed from these two laws using the Helmholtz's theorem. For example, since the magnetic field is divergence-free (Gauss's law for magnetism), i.e. ▽ · B = 0, A always exists that satisfies the above definition.

The vector potential A is used when studying the Lagrangian in classical mechanics and in quantum mechanics (see Schrödinger equation for charged particles, Dirac equation, Aharonov-Bohm effect).

In the SI system, the units of A are volt-seconds per metre (V·s·m⁻¹) and are the same as that of momentum per unit charge.

Although the magnetic field B is a pseudovector (also called axial vector), the vector potential A is not: A is a polar vector.^[2] This means that if the right-hand rule for cross products were replaced with a left-hand rule, but without changing any other equations or definitions, then B would switch signs, but A would not change. This is an example of a general theorem: The curl of a polar vector is a pseudovector, and vice-versa.^[2]

Gauge choices

Main article: Gauge fixing

The above definition does not define the magnetic vector potential uniquely because, by definition, we can arbitrarily add curl-free components to the magnetic potential without changing the observed magnetic field. Thus, there is a degree of freedom available when choosing A. This condition is known as gauge invariance.

Maxwell's equations in terms of vector potential

Using the above definition of the potentials and applying it to the other two Maxwell's equations (the ones that are not automatically satisfied) results in a complicated differential equation that can be simplified using the Lorenz gauge where A is chosen so as to satisfy:

$\nabla\cdot\textbf{A} %2B \frac{1}{c^2} \frac{\partial \phi}{\partial t} = 0.$ ^[1]

Using the Lorenz gauge, Maxwell's equations can be written compactly in terms of the magnetic vector potential A and the electric scalar potential Φ.

$\nabla^2\phi - \frac{1}{c^2}\frac{\partial^2 \phi}{\partial t^2} = - \rho/ \epsilon_0$ ^[1]

$\nabla^2\textbf{A} - \frac{1}{c^2}\frac{\partial^2 \textbf{A}}{\partial t^2} = - \mu_0 \textbf{J}$ ^[1]

In other gauges, the equations are different. A different notation to write these same equations (using four-vectors) is shown below.

Calculation of potentials from source distributions

Main article: Retarded potential

The solutions of Maxwell's equations (in the Lorenz gauge) Feynman ^[1] and Jackson^[3] with the boundary condition that both potentials go to zero sufficiently fast as they approach infinity are called the 'retarded potentials which are:

$\mathbf{A}(\mathbf{p_1},t) = \frac{\mu_0}{4\pi} \int_{V_2}\frac{\mathbf{j}(\mathbf{p_2},t_r)}{r_{12}}\,{\rm d}V$ where $t_r = t - \frac{r_{12}}{c}$

$\phi(\mathbf{p_1},t) = \frac{1}{4\pi\epsilon_0} \int_{V_2}\frac{\rho(\mathbf{p_2},t_r)}{r_{12}}\,{\rm d}V$

where

t is the time at which the value of A and 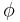$\phi\,$ are to be calculated.

p₁ is the point at which the value of A and 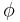$\phi\,$ are to be calculated.

p₂ is the integration variable.

r₁₂ is the distance from point p₁ to point p₂.

t_r is a time earlier than t by $\textstyle\frac{r_{12}}{c}$ which is the time it takes an effect generated at p₂ to propagate to p₁ at the speed of light. t_r is also called retarded time.

A ( p₁, t ) is the magnetic vector potential at point p₁ and time t.

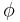$\phi\,$ ( p₁, t )is the electric scalar potential at point p₁ and time t.

j ( p₁, t_r ) is the current density at point p₂ and time t_r

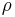$\rho\,$ ( p₁, t_r ) is the charge density at point p₂ and time t_r.

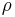V₂ is the volume of all points p₂ where $\mathbf{j}$ or $\rho\,$ is non-zero at least sometimes.

There are a few notable things about A and 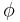$\phi\,$ calculated in this way:

(The Lorenz gauge condition): 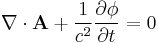$\nabla\cdot\mathbf{A} %2B \frac{1}{c^2}\frac{\partial\phi}{\partial t} = 0$ is satisfied.

The position of the source point p₂ only enters the equation as a scalar distance from p₁ to p₂. The direction from p₁ to p₂ does not enter into the equation. The only thing that matters about a source point is how far away it is.

The integrand uses retarded time. This simply reflects the fact that changes in the sources propagate at the speed of light

The equation for A is a vector equation. In Cartesian coordinates, the equation separates into three equations thus^[4]:

$\mathbf{A_x}(\mathbf{p_1},t) = \frac{\mu_0}{4\pi} \int_{V_2}\frac{\mathbf{j_x}(\mathbf{p_2},t_r)}{r_{12}}\,{\rm d}V$ where A_x and j_x are the components of A and j in the direction of the x axis.

$\mathbf{A_y}(\mathbf{p_1},t) = \frac{\mu_0}{4\pi} \int_{V_2}\frac{\mathbf{j_y}(\mathbf{p_2},t_r)}{r_{12}}\,{\rm d}V$

$\mathbf{A_z}(\mathbf{p_1},t) = \frac{\mu_0}{4\pi} \int_{V_2}\frac{\mathbf{j_z}(\mathbf{p_2},t_r)}{r_{12}}\,{\rm d}V$

In this form it is easy to see that the component of A in a given direction depends only on the components of $\mathbf{j}$ that are in the same direction. If the current is carried in a long straight wire, the A points in the same direction as the wire.

In other gauges the formula for A and 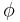$\phi \,$ is different—for example, see Coulomb gauge for another possibility.

Depiction of the A field

See Feynman^[5] for the depiction of the A field around a long thin solenoid.

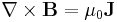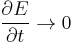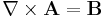Since $\nabla \times \mathbf{B} = \mu_0\mathbf{J} \$ (assuming quasi-static conditions, i.e. $\frac{\partial E}{\partial t}\rightarrow 0$ )and $\nabla \times \mathbf{A} = \mathbf{B} \$ , the lines and contours of A relate to B like the lines and contours of B relate to j. Thus, a depiction of the A field around a loop of B flux (as would be produced in a toroidal inductor) is qualitatively the same as the B field around a loop of current.

The figure to the left is an artist's depiction of the A field. The thicker lines indicate paths of higher average intensity (shorter paths have higher intensity so that the path integral is the same). The lines are just drawn to look good and impart general look of the A field.

The drawing tacitly assumes 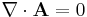$\nabla\cdot \mathbf{A} = 0$ . This would be true under the following assumptions:

the Coulomb gauge is assumed
the Lorenz gauge is assumed and there is no distribution of charge, $\rho = 0 \,$
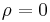
the Lorenz gauge is assumed and zero frequency is assumed
the Lorenz gauge is assumed and a non-zero frequency that is low enough to neglect 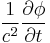$\frac{1}{c^2}\frac{\partial\phi}{\partial t}$ is assumed

Electromagnetic four-potential

Main article: Electromagnetic four-potential

In the context of special relativity, it is natural to join the magnetic vector potential together with the (scalar) electric potential into the electromagnetic potential, also called "four-potential".

One motivation for doing so is that the four-potential is a mathematical four-vector. Thus, using standard four-vector transformation rules, if the electric and magnetic potentials are known in one inertial reference frame, they can be simply calculated in any other inertial reference frame.

Another, related motivation is that the content of classical electromagnetism can be written in a concise and convenient form using the electromagnetic four potential, especially when the Lorenz gauge is used. In particular, in abstract index notation, the set of Maxwell's equations (in the Lorenz gauge) may be written (in Gaussian units) as follows:

$\partial^\mu A_\mu = 0 \,$

$\Box A_\mu = \frac{4 \pi}{c} J_\mu$

where □ is the d'Alembertian and J is the four-current. The first equation is the Lorenz gauge condition while the second contains Maxwell's equations.

Yet another motivation for creating the electromagnetic four-potential is that it plays a very important role in quantum electrodynamics.

Magnetic scalar potential

The magnetic scalar potential is another useful tool in describing the magnetic field, especially for permanent magnets.

In a simply connected domain where there is no free current,

$\nabla\times\mathbf{H}=0,$

hence we can define magnetic scalar potential ψ as^[6]

$\mathbf{H}=-\nabla\psi.$

And since

$\nabla\cdot\mathbf{B}=\mu_{0}\nabla\cdot(\mathbf{H%2BM})=0,$

it follows that

$\nabla^{2}\psi=-\nabla\cdot\mathbf{H}=\nabla\cdot\mathbf{M}.$

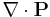Here $\nabla\cdot\mathbf{M}$ acts as the source for magnetic field, much like $\nabla\cdot\mathbf{P}$ as the source for electric field. So analogously to bound electric charge, we can call

$\rho_{m}=-\nabla\cdot\mathbf{M}$

bound magnetic charge.

If there is free current, one may subtract the contribution of free current per Biot-Savart law from total magnetic field and solve the remainder with the scalar potential method.

Notes

^ ^a ^b ^c ^d ^e ^f Feynman (1964, p. 15_15)
^ ^a ^b Tensors and pseudo-tensors, lecture notes by Richard Fitzpatrick
^ Jackson (1999, p. 246)
^ Kraus (1984, p. 189)
^ Feynman (1964, p. 15_11)
^ Vanderlinde (2005, pp. 194~199)

References

Duffin, W.J. (1990). Electricity and Magnetism, Fourth Edition. McGraw-Hill.

Feynman, Richard P; Leighton, Robert B; Sands, Matthew (1964). The Feynman Lectures on Physics Volume 2. Addison-Wesley. ISBN 020102117XP.

Jackson, John David (1998). Classical Electrodynamics, Third Edition. John Wiley & Sons.

Jackson, John Davd (1999), Classical Electrodynamics (3rd ed.), John-Wiley, ISBN 047130932X

Kraus, John D. (1984), Electromagnetics (3rd ed.), McGraw-Hill, ISBN 0070354235

Ulaby, Fawwaz (2007). Fundamentals of Applied Electromagnetics, Fifth Edition. Pearson Prentice Hall. pp. 226–228. ISBN 0-13-241326-4.

Vanderlinde, Jack (2005). Classical Electromagnetic Theory. ISBN 1-4020-2699-4. http://www.springerlink.com/index/10.1007/1-4020-2700-1.