MV-algebra
In abstract algebra, a branch of pure mathematics, an MV-algebra is an algebraic structure with a binary operation 
, a unary operation 
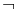, and the constant 
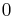, satisfying certain axioms. MV-algebras are models of Łukasiewicz logic; the letters MV refer to many-valued logic of Łukasiewicz.
Contents |
Definitions
An MV-algebra is an algebraic structure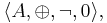 
consisting of
- a non-empty set
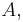
- a binary operation on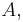
- a unary operati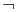on
on 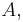and - a constant 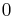denoting a fixed element of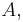
which satisfies the following identities:
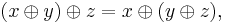
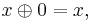
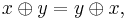
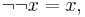
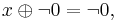and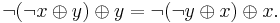
By virtue of the first three axioms,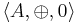 
is a commutative monoid. Being defined by identities, MV-algebras form a variety of algebras. The variety of MV-algebras is a subvariety of the variety of BL-algebras and contains all Boolean algebras.
An MV-algebra can equivalently be defined (Hájek 1998) as a prelinear commutative bounded integral residuated lattice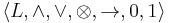 
satisfying the additional identity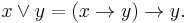 
Examples of MV-algebras
A simple numerical example is ![A=[0,1],](/2012-wikipedia_en_all_nopic_01_2012/I/0296682e2a43df25157421f698988f49.png)
with operations 
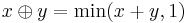and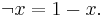 
In mathematical fuzzy logic, this MV-algebra is called the standard MV-algebra, as it forms the standard real-valued semantics of Łukasiewicz logic.
The trivial MV-algebra has the only element 0 and the operations defined in the only possible way,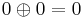 
and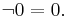 
The two-element MV-algebra is actually the two-element Boolean algebra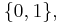 
with coinciding with Boolean disjunction and 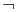with Boolean negation.
Other finite linearly ordered MV-algebras are obtained by restricting the universe and operations of the standard MV-algebra to the set of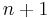 
equidistant real numbers between 0 and 1 (both included), that is, the set 
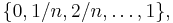which is closed under the operations and 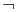of the standard MV-algebra.
Another important example is Chang's MV-algebra, consisting just of infinitesimals (with the order type ω) and their co-infinitesimals.
Relation to Łukasiewicz logic
Chang devised MV-algebras to study many-valued logics, introduced by Jan Łukasiewicz in 1920. In particular, MV-algebras form the algebraic semantics of Łukasiewicz logic, as described below.
Given an MV-algebra A, an A-valuation is a homomorphism from the algebra of propositional formulas (in the language consisting of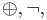 
and 0) into A. Formulas mapped to 1 (or 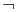0) for all A-valuations are called A-tautologies. If the standard MV-algebra over [0,1] is employed, the set of all [0,1]-tautologies determines so-called infinite-valued Łukasiewicz logic.
Chang's (1958, 1959) completeness theorem states that any MV-algebra equation holding in the standard MV-algebra over the interval [0,1] will hold in every MV-algebra. Algebraically, this means that the standard MV-algebra generates the variety of all MV-algebras. Equivalently, Chang's completeness theorem says that MV-algebras characterize infinite-valued Łukasiewicz logic, defined as the set of [0,1]-tautologies.
The way the [0,1] MV-algebra characterizes all possible MV-algebras parallels the well-known fact that identities holding in the two-element Boolean algebra hold in all possible Boolean algebras. Moreover, MV-algebras characterize infinite-valued Łukasiewicz logic in a manner analogous to the way that Boolean algebras characterize classical bivalent logic (see Lindenbaum-Tarski algebra).
References
- Chang, C. C. (1958) "Algebraic analysis of many-valued logics," Transactions of the American Mathematical Society 88: 476–490.
- ------ (1959) "A new proof of the completeness of the Lukasiewicz axioms," Transactions of the American Mathematical Society 88: 74–80.
- Cignoli, R. L. O., D'Ottaviano, I. M. L., Mundici, D. (2000) Algebraic Foundations of Many-valued Reasoning. Kluwer.
- Di Nola A., Lettieri A. (1993) "Equational characterization of all varieties of MV-algebras," Journal of Algebra 221: 123–131.
- Hájek, Petr (1998) Metamathematics of Fuzzy Logic. Kluwer.