Maximally stable extremal regions
| Feature detection |
|---|
|
Output of a typical corner detection algorithm
|
| Edge detection |
| Canny · Canny-Deriche · Differential · Sobel · Prewitt · Roberts Cross |
| Interest point detection |
| Corner detection |
| Harris operator · Shi and Tomasi · Level curve curvature · SUSAN · FAST |
| Blob detection |
| Laplacian of Gaussian (LoG) · Difference of Gaussians (DoG) · Determinant of Hessian (DoH) · Maximally stable extremal regions · PCBR |
| Ridge detection |
| Hough transform |
| Structure tensor |
| Affine invariant feature detection |
| Affine shape adaptation · Harris affine · Hessian affine |
| Feature description |
| SIFT · SURF · GLOH · HOG · LESH |
| Scale-space |
| Scale-space axioms · Implementation details · Pyramids |
In computer vision, maximally stable extremal regions (MSER) are used as a method of blob detection in images. This technique was proposed by Matas et al.[1] to find correspondences between image elements from two images with different viewpoints. This method of extracting a comprehensive number of corresponding image elements contributes to the wide-baseline matching, and it has led to better stereo matching and object recognition algorithms.
Contents |
Terms and Definitions
Image  is a mapping
is a mapping 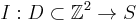 . Extremal regions are well defined on images if:
. Extremal regions are well defined on images if:
 is totally ordered (reflexive, antisymmetric and transitive binary relations
is totally ordered (reflexive, antisymmetric and transitive binary relations 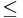 exist).
exist).- An adjacency relation
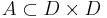 is defined.
is defined.
Region  is a contiguous subset of
is a contiguous subset of  . (For each
. (For each 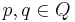 there is a sequence
there is a sequence 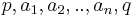 and
and 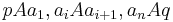 .
.
(Outer) Region Boundary 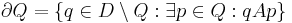 , which means the boundary
, which means the boundary 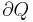 of
of  is the set of pixels adjacent to at least one pixel of
is the set of pixels adjacent to at least one pixel of  but not belonging to
but not belonging to  .
.
Extremal Region 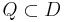 is a region such that either for all
is a region such that either for all 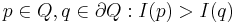 (maximum intensity region) or for all
(maximum intensity region) or for all 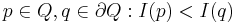 (minimum intensity region).
(minimum intensity region).
Maximally Stable Extremal Region Let 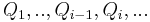 be a sequence of nested extremal regions (
be a sequence of nested extremal regions (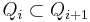 ). Extremal region
). Extremal region 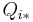 is maximally stable if and only if
is maximally stable if and only if 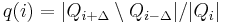 has a local minimum at
has a local minimum at 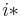 . (Here
. (Here  denotes cardinality.)
denotes cardinality.)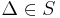 is a parameter of the method.
is a parameter of the method.
The concept more simply can be explained by thresholding. All the pixels below a given threshold are 'black' and all those above or equal are 'white'. If we are shown a sequence of thresholded images 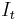 with frame
with frame  corresponding to threshold t, we would see first a white image, then 'black' spots corresponding to local intensity minima will appear then grow larger. These 'black' spots will eventually merge, until the whole image is black. The set of all connected components in the sequence is the set of all extremal regions. In that sense, the concept of MSER is linked to the one of component tree of the image.[2] The component tree indeed provide an easy way for implementing MSER.[3]
corresponding to threshold t, we would see first a white image, then 'black' spots corresponding to local intensity minima will appear then grow larger. These 'black' spots will eventually merge, until the whole image is black. The set of all connected components in the sequence is the set of all extremal regions. In that sense, the concept of MSER is linked to the one of component tree of the image.[2] The component tree indeed provide an easy way for implementing MSER.[3]
Extremal regions
Extremal regions in this context have two important properties, that the set is closed under...
- continuous (and thus projective) transformation of image coordinates. This means it is affine invariant and it doesn't matter if the image is warped or skewed.
- monotonic transformation of image intensities. The approach is of course sensitive to natural lighting effects as change of day light or moving shadows.
Advantages of MSER
Because the regions are defined exclusively by the intensity function in the region and the outer border, this leads to many key characteristics of the regions which make them useful. Over a large range of thresholds, the local binarization is stable in certain regions, and have the properties listed below.
- Invariance to affine transformation of image intensities
- Covariance to adjacency preserving (continuous)transformation
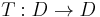 on the image domain
on the image domain - Stability: only regions whose support is nearly the same over a range of thresholds is selected.
- Multi-scale detection without any smoothing involved, both fine and large structure is detected.
Note however that detection of MSERs in a scale pyramid improves repeatability, and number of correspondences across scale changes.[4] - The set of all extremal regions can be enumerated in worst-case
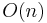 , where
, where  is the number of pixels in the image.[5]
is the number of pixels in the image.[5]
Comparison to other region detectors
In Mikolajczyk et al.,[6] six region detectors are studied (Harris-affine, Hessian-affine, MSER, edge-based regions, intensity extrema, and salient regions). A summary of MSER performance in comparison to the other five follows.
- Region density - in comparison to the others MSER offers the most variety detecting about 2600 regions for a textured blur scene and 230 for a light changed. scene, and variety is generally considered to be good. Also MSER had a repeatability of 92% for this test.
- Region size - MSER tended to detect many small regions, versus large regions which are more likely to be occluded or to not cover a planar part of the scene. Though large regions may be slightly easier to match.
- Viewpoint change - MSER outperforms the five other region detectors in both the original images and those with repeated texture motifs.
- Scale change - Following Hessian-affine detector, MSER comes in second under a scale change and in-plane rotation.
- Blur - MSER proved to be the most sensitive to this type of change in image, which is the only area that this type of detection is lacking in.
Note however that this evaluation did not make use of multi-resolution detection, which has been shown to improve repeatability under blur.[4] - Light change - MSER showed the highest repeatability score for this type of scene, with all the other having good robustness as well.
MSER consistently resulted in the highest score through many tests, proving it to be a reliable region detector.[6]
Implementation
The original algorithm of Matas et al.[1] is 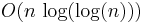 in the number
in the number 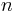 of pixels, which is almost linear. It proceeds by first sorting the pixels by intensity. This would take
of pixels, which is almost linear. It proceeds by first sorting the pixels by intensity. This would take 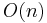 time, using BINSORT. After sorting, pixels are marked in the image, and the list of growing and merging connected components and their areas is maintained using the union-find algorithm. This would take
time, using BINSORT. After sorting, pixels are marked in the image, and the list of growing and merging connected components and their areas is maintained using the union-find algorithm. This would take 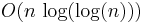 time. In practice these steps are very fast. During this process, the area of each connected component as a function of intensity is stored producing a data structure. A merge of two components is viewed as termination of existence of the smaller component and an insertion of all pixels of the smaller component into the larger one. In the extremal regions, the 'maximally stable' ones are those corresponding to thresholds where the relative area change as a function of relative change of threshold is at a local minimum, i.e. the MSER are the parts of the image where local binarization is stable over a large range of thresholds.[1][6]
time. In practice these steps are very fast. During this process, the area of each connected component as a function of intensity is stored producing a data structure. A merge of two components is viewed as termination of existence of the smaller component and an insertion of all pixels of the smaller component into the larger one. In the extremal regions, the 'maximally stable' ones are those corresponding to thresholds where the relative area change as a function of relative change of threshold is at a local minimum, i.e. the MSER are the parts of the image where local binarization is stable over a large range of thresholds.[1][6]
The component tree is the set of all connected components of the thresholds of the image, ordered by inclusion. Efficient (quasi-linear whatever the range of the weights) algorithms for computing it do exist.[2] Thus this structure offers an easy way for implementing MSER.[3]
More recently, Nister and Stewenius have proposed a truly (if the weight are small integers) worst-case 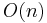 method in,[5] which is also much faster in practice. This algorithm is similar to the one of Ph. Salembier et al. [7].
method in,[5] which is also much faster in practice. This algorithm is similar to the one of Ph. Salembier et al. [7].
Robust wide-baseline algorithm
The purpose of this algorithm is to match MSERs to establish correspondence points between images. First MSER regions are computed on the intensity image (MSER+) and on the inverted image (MSER-). Measurement regions are selected at multiple scales: the size of the actual region, 1.5x, 2x, and 3x scaled convex hull of the region. Matching is accomplished in a robust manner, so it is better to increase the distinctiveness of large regions without being severely affected by clutter or non-planarity of the region's pre-image. A measurement taken from an almost planar patch of the scene with stable invariant description are called a 'good measurement'. Unstable ones or those on non-planar surfaces or discontinuities are called 'corrupted measurements'. The robust similarity is computed: For each 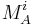 on region
on region 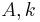 regions
regions  from the other image with the corresponding i-th measurement
from the other image with the corresponding i-th measurement 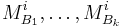 nearest to
nearest to 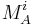 are found and a vote is cast suggesting correspondence of A and each of
are found and a vote is cast suggesting correspondence of A and each of  . Votes are summed over all measurements, and using probability analysis, we pick out the 'good measurements' as the 'corrupt measurements' will likely spread their votes randomly. By applying RANSAC to the centers of gravity of the regions, we can compute a rough epipolar geometry. An affine transformation between pairs of potentially corresponding regions is computed, and correspondences define it up to a rotation, which is then determined by epipolar lines. The regions are then filtered, and the ones with correlation of their transformed images above a threshold are chosen. RANSAC is applied again with a more narrow threshold, and the final eipolar geometry is estimated by the eight-point algorithm.
. Votes are summed over all measurements, and using probability analysis, we pick out the 'good measurements' as the 'corrupt measurements' will likely spread their votes randomly. By applying RANSAC to the centers of gravity of the regions, we can compute a rough epipolar geometry. An affine transformation between pairs of potentially corresponding regions is computed, and correspondences define it up to a rotation, which is then determined by epipolar lines. The regions are then filtered, and the ones with correlation of their transformed images above a threshold are chosen. RANSAC is applied again with a more narrow threshold, and the final eipolar geometry is estimated by the eight-point algorithm.
This algorithm can be tested here (Epipolar or homography geometry constrained matches): [WBS Image Matcher [1]
Extensions and Adaptations
- The MSER algorithm has been adapted to colour images, by replacing thresholding of the intensity function with agglomerative clustering, based on colour gradients.[8]
- The MSER algorithm can be used to track colour objects, by performing MSER detection on the Mahalanobis distance to a colour distribution.[3]
- By detecting MSERs in multiple resolutions, robustness to blur, and scale change can be improved.[4]
Other Applications
- Shape Descriptors for Maximally Stable Extremal Regions
- Efficient Maximally Stable Extremal Region (MSER) Tracking
- N-tree Disjoint-Set Forests for Maximally Stable Extremal Regions
- Video Google and Object Level Grouping for Video Shots
- Real-Time Extraction of Maximally Stable Extremal Regions on an FPGA
- Maximally Stable Colour Regions for Recognition and Matching
See also
External links
- VLFeat, an open source computer vision library in C (with a MEX interface to MATLAB), including an implementation of MSER
- OpenCV, an open source computer vision library in C/C++, including an implementation of Linear Time MSER
- Detector Repeatabilty Study, Kristian Mikolajczyk Binaries (Win/Linux to compute MSER/HarrisAffine... . Binary used in his repeatability study.
References
- ^ a b c J. Matas, O. Chum, M. Urba, and T. Pajdla. "Robust wide baseline stereo from maximally stable extremal regions." Proc. of British Machine Vision Conference, pages 384-396, 2002.
- ^ a b L. Najman and M. Couprie: "Building the component tree in quasi-linear time"; IEEE Transaction on Image Processing, Volume 15, Numbers 11 , 2006, pp 3531-3539
- ^ a b c Donoser, M. and Bischof, H. Efficient Maximally Stable Extremal Region (MSER) Tracking CVPR, 2006.
- ^ a b c Forssen, P-E. and Lowe, D.G. "Shape Descriptors for Maximally Stable Extremal Regions" ICCV, 2007.
- ^ a b Nister, D. and Stewenius, H., "Linear Time Maximally Stable Extremal Regions", ECCV, 2008.
- ^ a b c K. Mikolajczyk, T. Tuytelaars, C. Schmid, A. Zisserman, T. Kadir and L. Van Gool: "A Comparison of Affine Region Detectors"; International Journal of Computer Vision, Volume 65, Numbers 1-2 / November, 2005, pp 43-72
- ^ Salembier, Philippe; A. Oliveras and L. Garrido (1998). "Anti-extensive Connected Operators for Image and Sequence Processing". IEEE Transactions on Image Processing 7 (4): 555-570. http://imatge.upc.edu/pub/ps/IEEE_IP98_Salembier_Oliveras_Garrido.ps.gz.
- ^ Forssen, P-E. Maximally Stable Colour Regions for Recognition and Matching, CVPR, 2007.