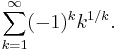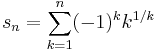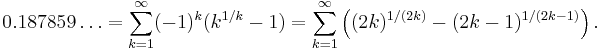MRB constant

The MRB constant, named after Marvin Ray Burns, is a mathematical constant for which no closed-form expression is known. It is not known whether the MRB constant is algebraic, transcendental, or even irrational.

The numerical value of MRB constant, truncated to 6 decimal places, is

0.187859… (sequence A037077 in OEIS).

Contents

Definition

The MRB constant is related to the following divergent series:

\sum_{k=1}^{\infty} (-1)^k k^{1/k}.

Its partial sums

s_n = \sum_{k=1}^n (-1)^k k^{1/k}

are bounded so that their limit points form an interval [−0.812140…,0.187859…] of length 1. The upper limit point 0.187859… is what is known as the MRB constant.[1]

The MRB constant can be explicitly defined by the following infinite sums:[2]

0.187859\ldots = \sum_{k=1}^{\infty} (-1)^k (k^{1/k} - 1) = \sum_{k=1}^{\infty} \left((2k)^{1/(2k)} - (2k-1)^{1/(2k-1)}\right).

There is no known closed-form expression of the MRB constant.[3]

History

Marvin Ray Burns published his discovery of the constant in 1999. The discovery is a result of a "math binge" that started in the spring of 1994.[4] Before verifying with colleague Simon Plouffe that such a constant had not already been discovered or at least not widely published, Burns called the constant "rc" for root constant.[5] At Plouffe's suggestion, the constant was renamed Marvin Ray Burns's Constant, and then shortened to "MRB constant" in 1999.[6]

References

  1. ^ Burns, Marvin R. (1999-09-01). "MRB Constant". Plouffe's Inverter. http://pi.lacim.uqam.ca:16080/piDATA/mrburns.txt. Retrieved 2009-05-05. 
  2. ^ Weisstein, Eric W., "MRB Constant" from MathWorld.
  3. ^ Finch, Steven R. (2003). Mathematical Constants. Cambridge, England: Cambridge University Press. p. 450. ISBN 0521818052. 
  4. ^ Burns, Marvin R. (2002-04-12). "Captivity’s Captor: Now is the Time for the Chorus of Conversion". Indiana University. https://oncourse.iu.edu/access/content/user/marburns/Filemanager_Public_Files/final1.doc. Retrieved 2009-05-05. 
  5. ^ Burns, Marvin R. (1999-01-23). "RC". math2.org. http://math2.org/mmb/thread/901. Retrieved 2009-05-05. 
  6. ^ Plouffe, Simon (1999-11-20). "Tables of Constants". Laboratoire de combinatoire et d'informatique mathématique. http://pi.lacim.uqam.ca/eng/table_en.html. Retrieved 2009-05-05. 

External links