Luneburg lens
A Luneburg lens (originally Lüneburg lens, often incorrectly spelt Luneberg lens) is a spherically symmetric, variable-index refracting structure which will form perfect geometrical images of two given concentric spheres onto each other. The Luneburg lens is a spherical lens (usually a ball lens) generally having a gradient of decreasing refractive index n radially out from its center. The focusing properties of the Luneburg lens can be achieved through an infinite number of refractive-index solutions. The simplest such solution was proposed by Rudolf Luneburg in 1944.[1] Luneburg's solution for the refractive-index creates two conjugate foci outside of the lens. The solution takes a simple and explicit form if one focal point lies at infinity, and the other on the opposite surface of the lens. J. Brown and A. S. Gutman subsequently proposed solutions which generate one internal focal point and one external focal point.[2][3] These solutions are not unique; the set of solutions are defined by a set of definite integrals which must be evaluated numerically.[4]
Like a Luneburg lens, a gravitational lens also has a radially decreasing refractive index.
Contents |
Luneburg's solution
Each point on the surface of an ideal Luneburg lens is the focal point for parallel radiation incident on the opposite side. Ideally, the dielectric constant 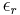 of the material composing the lens falls from 2 at its center to 1 at its surface (or equivalently, the refractive index
of the material composing the lens falls from 2 at its center to 1 at its surface (or equivalently, the refractive index  falls from
falls from 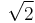 to 1), according to
to 1), according to
where  is the radius of the lens. Because the refractive index at the surface is the same as a that of the surrounding medium, no reflection occurs at the surface. Within the lens, the paths of the rays are arcs of ellipses.
is the radius of the lens. Because the refractive index at the surface is the same as a that of the surrounding medium, no reflection occurs at the surface. Within the lens, the paths of the rays are arcs of ellipses.
The practical implementation is normally a layered structure of discrete concentric shells, each of a different refractive index. These shells form a stepped refractive index profile that differs slightly from Luneburg's solution. This kind of lens is usually employed for microwave frequencies, especially to construct efficient microwave antennas and radar calibration standards.
Luneburg lens radar reflector
A radar reflector can be made from a Luneburg lens by metallizing parts of its surface. Radiation from a distant radar transmitter is focussed onto the underside of the metallization on the opposite side of the lens; here it is reflected, and focussed back onto the radar station. A difficulty with this scheme is that metallized regions block the entry or exit of radiation on that part of the lens, but the non-metallized regions result in a blind-spot on the opposite side.
Maxwell's fish-eye
Maxwell's fish-eye is also an example of the generalized Luneburg lens. The fish-eye, which was first fully described by Maxwell in 1854[5] (and therefore pre-dates Luneburg's solution), has a refractive index varying according to
 .
.
It focuses each point on the spherical surface of radius R to the opposite point on the same surface. Within the lens, the paths of the rays are arcs of circles.
Publication and attribution
The properties of this lens are described in one of a number of set problems or puzzles in the 1853 Cambridge and Dublin Mathematical Journal.[6] The challenge is to find the refractive index as a function of radius, given that a ray describes a circular path, and further to prove the focusing properties of the lens. The solution is given in the 1854 edition of the same journal.[5] The problems and solutions were originally published anonymously, but the solution of this problem (and one other) were included in Niven's The Scientific Papers of James Clerk Maxwell,[7] which was published eleven years after Maxwell's death.
Luneburg lens satellite antenna
A Luneburg lens made of polyethylene and polystyrene has been designed for train-mounted satellite dishes. The hemispherical Luneburg lens design is smaller and more reliable than traditional satellite dish antennas.[8][9]
See also
References
- ^ Luneburg, R. K. (1944). Mathematical Theory of Optics. Providence, Rhode Island: Brown University. pp. 189–213.
- ^ Brown, J. (1953). Wireless Engineer 30: 250.
- ^ Gutman, A. S. (1954). "Modified Luneberg Lens". J. Appl. Phys. 25: 855. Bibcode 1954JAP....25..855G. doi:10.1063/1.1721757.
- ^ Morgan, S. P. (1958). "General solution of the Luneburg lens problem". J. Appl. Phys. 29: 1358–1368. Bibcode 1958JAP....29.1358M. doi:10.1063/1.1723441.
- ^ a b "Solutions of problems (prob. 3, vol. VIII. p. 188)". The Cambridge and Dublin mathematical journal (Macmillan) 9: 9–11. 1854. http://books.google.com/books?id=-bI5AAAAMAAJ&pg=PA9.
- ^ "Problems (3)". The Cambridge and Dublin mathematical journal (Macmillan) 8: 188. 1853. http://books.google.com/books?id=1xoAAAAAMAAJ&pg=PA188.
- ^ Niven, ed (1890). The Scientific Papers of James Clerk Maxwell. New York: Dover Publications. p. 76. http://www.archive.org/stream/scientificpapers01maxw#page/76.
- ^ Kremen, Rachel (December 30, 2008). "Broadband on Rails: A compact lens could make high-speed Internet access commonplace on trains". Technology Review. MIT. http://technologyreview.com/communications/21912/?a=f. Retrieved 20 August 2009.
- ^ Caille, Gérard; et al. (2004). Hemispherical Luneberg antenna motorized for satellite reception from the roof of a vehicle.. http://www.radar-reflector.com/wp-content/uploads/2008/09/jina_gb.pdf. Retrieved August 20, 2009.
