Ludwig Schläfli

Ludwig Schläfli (15 January 1814 – 20 March 1895) was a Swiss geometer and complex analyst (at the time called function theory) who was one of the key figures in developing the notion of higher dimensional spaces. The concept of multidimensionality has since come to play a pivotal role in physics, and is a common element in science fiction. Although his ideas have become so widely accepted, he is poorly remembered, even among mathematicians.

Contents

Life and career

Youth and education

Ludwig Schläfli spent most of his life in Switzerland. He was born in Graßwil, his mother's hometown. The family then moved to the nearby Burgdorf, where his father worked as a tradesman. His father wanted Ludwig to follow in his footsteps, but Ludwig was not cut out for practical work.

In contrast, because of his mathematical gifts, he was allowed to attend the Gymnasium in Bern in 1829. By that time he was already learning differential calculus from Abraham Gotthelf Kästner's Mathematische Anfangsgründe der Analysis des Unendlichen (1761). In 1831 he transferred to the Akademie in Bern for further studies. By 1834 the Akademie had become the new Universität Bern, where he started studying theology.

Teaching

After his graduation in 1836, he was appointed a secondary school teacher in Thun. He stayed there until 1847, spending his free time studying mathematics and botany while attending the university in Bern once a week.

A turning point in his life came in 1843. Schläfli had planned to visit Berlin and become acquainted with its mathematical community, especially Jakob Steiner, a well known Swiss mathematician. But unexpectedly Steiner showed up in Bern and they met. Not only was Steiner impressed by Schläfli's mathematical knowledge, he was also very interested in Schläfli's fluency in Italian and French.

Steiner proposed Schläfli to assist his Berlin colleagues Carl Gustav Jacob Jacobi, Dirichlet, Carl Wilhelm Borchardt and himself as an interpreter on a forthcoming trip to Italy. Steiner sold this idea to his friends on the following way, which indicates Schläfli must have been somewhat clumsy at daily affairs:

... während er den Berliner Freunden den neugeworbenen Reisegefaehrten durch die Worte anpreis, der sei ein ländlicher Mathematiker bei Bern, für die Welt ein Esel, aber Sprachen lerne er wie ein Kinderspiel, den wollten sie als Dolmetscher mit sich nehmen. [ADB]

English translation:

... while he (Steiner) praised/recommended the new travel companion to his Berlin friends with the words that he (Schläfli) was a provincial mathematician working near Bern, an 'ass for the world' (i.e. not very practical), but that he learned languages like child's play, and that they should take him with them as a translator.

Schläfli accompanied them to Italy, and benefited much from the trip. They stayed for more than six months, during which time Schläfli even translated some of the others' mathematical works into Italian.

Later life

Schläfli kept up a correspondence with Steiner till 1856. The vistas that had been opened up to him encouraged him to apply for a position at the university in Bern in 1847, where he was appointed(?) in 1848. He stayed until his retirement in 1891, and spent his remaining time studying Sanskrit and translating the Hindu scripture Rig Veda into German, until his death in 1895.

Higher dimensions

Schläfli is one of the three architects of multidimensional geometry, together with Arthur Cayley and Bernhard Riemann. Around 1850 the general concept of Euclidean space hadn't been developed — but linear equations in n variables were well-understood. In the 1840s William Rowan Hamilton had developed his quaternions and John T. Graves and Arthur Cayley the octonions. The latter two systems worked with bases of four (respectively eight) elements, and suggested an interpretation analogous to the cartesian coordinates in three-dimensional space.

From 1850 to 1852 Schläfli worked on his magnum opus, Theorie der vielfachen Kontinuität, in which he initiated the study of the linear geometry of n-dimensional space. He also defined the n-dimensional sphere and calculated its volume. He then wanted to have this work published. It was sent to the Akademie in Vienna, but was refused because of its size. Afterwards it was sent to Berlin, with the same result. After a long bureaucratic pause, Schläfli was asked in 1854 to write a shorter version, but this he understandably did not. Steiner then tried to help him getting the work published in Crelle's journal, but somehow things didn't work out. The exact reasons remain unknown. Portions of the work were published by Cayley in English in 1860. The first publication of the entire manuscript was only in 1901, after Schläfli's death. The first review of the book then appeared in the Dutch mathematical journal Nieuw Archief voor de Wiskunde in 1904, written by the Dutch mathematician Pieter Hendrik Schoute.

During this period, Riemann held his famous Habilitationsvortrag Über die Hypothesen welche der Geometrie zu Grunde liegen in 1854, and introduced the concept of an n-dimensional manifold. The concept of higher dimensional spaces was starting to flourish.

Below is an excerpt from the preface to Theorie der vielfachen Kontinuität:

Anzeige einer Abhandlung über die Theorie der vielfachen Kontinuität
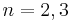Die Abhandlung, die ich hier der Kaiserlichen Akademie der Wissenschaften vorzulegen die Ehre habe, enthält einen Versuch, einen neuen Zweig der Analysis zu begründen und zu bearbeiten, welcher, gleichsam eine analytische Geometrie von n Dimensionen, diejenigen der Ebene und des Raumes als spezielle Fälle fuer n=2,3 in sich enthielte. Ich nenne denselben Theorie der vielfachen Kontinuität überhaupt in demselben Sinne, wie man zum Beispiel die Geometrie des Raumes eine Theorie der dreifachen Kontinuität nennen kann. Wie in dieser eine Gruppe von Werten der drei Koordinaten einen Punkt bestimmt, so soll in jener eine Gruppe gegebener Werte der n Variabeln 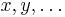x,y,\ldots eine Lösung bestimmen. Ich gebrauche diesen Ausdruck, weil man bei einer oder mehreren Gleichungen mit vielen Variabeln jede genügende Gruppe von Werten auch so nennt; das Ungewöhnliche der Benennung liegt nur darin, daß ich sie auch noch beibehalte, wenn gar keine Gleichung zwischen den Variabeln gegeben ist. In diesem Falle nenne ich die Gesamtheit aller Lösungen die n-fache Totalität; sind hingegen 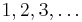1,2,3, \ldots Gleichungen gegeben, so heißt bzw. die Gesamtheit ihrer Lösungen 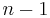n-1-faches, n-2-faches, n-3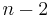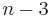-faches, ... Kontinuum. Aus der Vorstellung der allseitigen Kontinuität der in einer Totalität enthaltenen Lösungen entwickelt sich diejenige der Unabhängigkeit ihrer gegenseitigen Lage von dem System der gebrauchten Variabeln, insofern durch Transformation neue Variabeln an ihre Stelle treten können. Diese Unabhängigkeit spricht sich aus in der Unveränderlichkeit dessen, was ich den Abstand zweier gegebener Lösungen (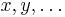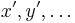x,y,\ldots), (x', y',\ldots) nenne und im einfachsten Fall durch
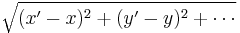
\sqrt{(x'-x)^2 %2B (y'-y)^2 %2B \cdots}
definiere, indem ich gleichzeitig das System der Variabeln ein orthogonales heiße, [...]

English translation:

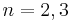The treatise I have the honour of presenting to the Imperial Academy of Science here, is an attempt to found and develop a new branch of analysis that would, as it were, be a geometry of n dimensions, containing the geometry of the plane and space as special cases for n=2,3. I call this the theory of multiple continuity in generally the same sense, in which one can call the geometry of space that of triple continuity. 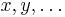Like in that theory the 'group' of values of its coordinates determines a point, so in this one a 'group' of given values of the n variables x,y,\ldots will determine a solution. I use this expression, because one also calls every sufficient 'group' of values thus in the case of one or more equations with many variables; the only thing unusual about this naming is, that I keep it when no equations between the variables is given whatsoever. In this case I call the total (set) of solutions the n-fold totality; whereas when 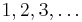1,2,3,\ldots equations are given, the total of their solutions is called respectively (an) 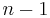n-1-fold, n-2-fold, n-3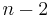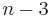-fold, … Continuum. From the notion of the solutions contained in a totality comes forth that of the independence of their relative positions (of the variables) in the system of variables used, insofar as new variables could take their place by transformation. This independence is expressed in the inalterability of that, which I call the distance between two given solutions (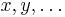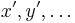x,y,\ldots), (x', y',\ldots) and define in the easiest case by:
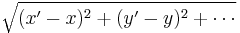
\sqrt{(x'-x)^2 %2B (y'-y)^2 %2B \cdots}
while at the same time I call a system of variables orthogonal [...]

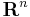We can see how he is still thinking of points in n-dimensional space as solutions to linear equations, and how he is considering a system without any equations, thus obtaining all possible points of the \mathbf{R}^n, as we would put it now. He disseminated the concept in the articles he published in the 1850s and 1860s, and it matured rapidly. By 1867 he starts an article by saying "We consider the space of n-tuples of points. [...]". This indicates not only that he had a firm grip on things, but also that his audience did not need a long explanation of it.

Polytopes

In Theorie der Vielfachen Kontinuität he goes on to define what he calls polyschemes, nowadays called polytopes, which are the higher dimensional analogues to polygons and polyhedra. He develops their theory and finds, among other things, the higher dimensional version of Euler's formula. He determines the regular polytopes, i.e. the n-dimensional cousins of regular polygons and platonic solids. It turns out there are six in dimension four and three in all higher dimensions.

Although Schläfli was familiar to his colleagues in the second half of the century, especially for his contributions to complex analysis, his early geometrical work didn't get proper attention for a long time. At the beginning of the twentieth century Pieter Hendrik Schoute started to work on polytopes together with Alicia Boole Stott. She reproved Schläfli's result on regular polytopes for dimension 4 only and afterwards rediscovered his book. Later Willem Abraham Wijthoff studied semi-regular polytopes and this work was continued by H.S.M. Coxeter, John Conway and others. There are still many problems to be solved in this area of investigation opened up by Ludwig Schläfli.

See also

Literature

External links