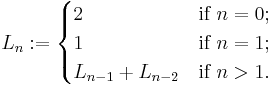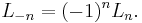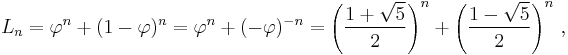Lucas number

The Lucas numbers are an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–1891), who studied both that sequence and the closely related Fibonacci numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences.

1 Definition
2 Extension to negative integers
3 Relationship to Fibonacci numbers
4 Congruence relation
5 Lucas primes
6 Lucas polynomials
7 See also
8 References
9 External links

Definition

Like the Fibonacci numbers, each Lucas number is defined to be the sum of its two immediate previous terms, i.e. it is a Fibonacci integer sequence. Consequently, the ratio between two consecutive Lucas numbers converges to the golden ratio. However, the first two Lucas numbers are L₀ = 2 and L₁ = 1 instead of 0 and 1, and the properties of Lucas numbers are therefore somewhat different from those of Fibonacci numbers.

A Lucas number may thus be defined as follows:

$L_n�:= \begin{cases} 2 & \mbox{if } n = 0; \\ 1 & \mbox{if } n = 1; \\ L_{n-1}%2BL_{n-2} & \mbox{if } n > 1. \\ \end{cases}$

The sequence of Lucas numbers begins:

2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, ... (sequence A000032 in OEIS).

Extension to negative integers

Using L_n-2 = L_n - L_n-1, one can extend the Lucas numbers to negative integers to obtain a doubly infinite sequence :

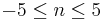..., -11, 7, -4, 3, -1, 2, 1, 3, 4, 7, 11, ... (terms $L_n$ for $-5\leq{}n\leq5$ are shown).

The formula for terms with negative indices in this sequence is

$L_{-n}=(-1)^nL_n.\!$

Relationship to Fibonacci numbers

The Lucas numbers are related to the Fibonacci numbers by the identities

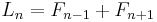
$\,L_n = F_{n-1}%2BF_{n%2B1}$
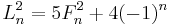$\,L_n^2 = 5 F_n^2 %2B 4 (-1)^n$ , and thus as 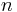$n\,$ approaches +∞, the ratio 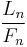$\frac{L_n}{F_n}$ approaches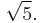 $\sqrt{5}.$
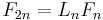
$\,F_{2n} = L_n F_n$
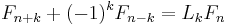
$\,F_{n%2Bk} %2B (-1)^k F_{n-k} = L_k F_n$
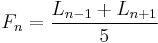
$\,F_n = {L_{n-1}%2BL_{n%2B1} \over 5}$

Their closed formula is given as:

$L_n = \varphi^n %2B (1-\varphi)^{n} = \varphi^n %2B (- \varphi)^{- n}=\left({ 1%2B \sqrt{5} \over 2}\right)^n %2B \left({ 1- \sqrt{5} \over 2}\right)^n\, ,$

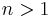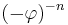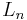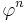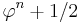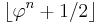where $\varphi$ is the Golden ratio. Alternatively, as for $n>1$ the magnitude of the term $(-\varphi)^{-n}$ is less than 1/2, $L_n$ is the closest integer to $\varphi^n$ or, equivalently, the integer part of $\varphi^n%2B1/2$ , also written as $\lfloor \varphi^n%2B1/2 \rfloor$ .

Conversely, 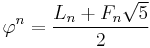$\varphi^n = {{L_n %2B F_n \sqrt{5}} \over 2}$ .

Congruence relation

L_n is congruent to 1 mod n if n is prime, but some composite values of n also have this property.

Lucas primes

A Lucas prime is a Lucas number that is prime. The first few Lucas primes are

2, 3, 7, 11, 29, 47, 199, 521, 2207, 3571, 9349, ... (sequence A005479 in OEIS).

If L_n is prime then n is either 0, prime, or a power of 2.^[1] L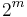 is prime for $m$ = 1, 2, 3, and 4 and no other known values of $m$ .

Lucas polynomials

In the same way as Fibonacci polynomials are derived from the Fibonacci numbers, the Lucas polynomials L_n(x) are a polynomial sequence derived from the Lucas numbers

References

^ Chris Caldwell, "The Prime Glossary: Lucas prime" from The Prime Pages.