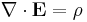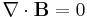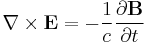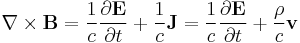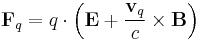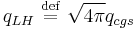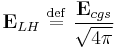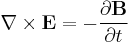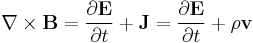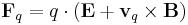Lorentz–Heaviside units

Lorentz–Heaviside units (or Heaviside–Lorentz units) are a system of units (particularly electromagnetic units) within cgs, named for Hendrik Antoon Lorentz and Oliver Heaviside. They are often used in relativistic calculations. They share with CGS-Gaussian units the property that the electric constant ε₀ and magnetic constant µ₀ do not exist; having been incorporated implicitly into the unit system. Consequently Lorentz–Heaviside differ by factors of 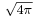$\scriptstyle \sqrt{4\pi}$ in the definitions of the electric and magnetic fields and of electric charge. They are particularly convenient when performing calculations in spatial dimensions greater than three such as is done in string theory.

Lorentz–Heaviside units, like SI units but unlike Gaussian units, are "rationalized", meaning that there are no factors of 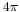$\scriptstyle 4\pi$ that appear explicitly in Maxwell's equations.^[1]^[2] The fact that these units are rationalized partly explains their appeal in quantum field theory: The Lagrangian underlying the theory does not have any factors of 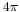$\scriptstyle 4\pi$ in these units.^[1]

Lorentz–Heaviside units may be combined with natural units in which 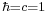$\scriptstyle \hbar=c=1$ also.

Maxwell's equations with sources

Maxwell's equations in free space with sources take the following form:

$\nabla \cdot \mathbf{E} = \rho \,$

$\nabla \cdot \mathbf{B} = 0 \,$

$\nabla \times \mathbf{E} = -\frac{1}{c} \frac{\partial \mathbf{B}} {\partial t} \,$

$\nabla \times \mathbf{B} = \frac{1}{c} \frac{ \partial \mathbf{E}} {\partial t} %2B \frac{1}{c} \mathbf{J} = \frac{1}{c} \frac{ \partial \mathbf{E}} {\partial t} %2B \frac{\rho}{c} \mathbf{v} \,$

where c is the speed of light in vacuum. Here E is the electric field, B is the magnetic field, ρ is charge density, J=ρv is current density, and v is the velocity of the distributed charge flowing as the current at the point where these equations are acting.

The Lorentz force equation is:

$\mathbf{F}_q = q \cdot \left(\mathbf{E} %2B \frac{\mathbf{v}_q}{c} \times \mathbf{B}\right) \,$

here q is a the charge of a test particle with vector velocity v_q and F_q is the combined electric and magnetic force acting on that test particle.

The charge and fields in Lorentz–Heaviside units are related to the quantities in cgs units by

$q_{LH} \ \stackrel{\mathrm{def}}{=}\ \sqrt{4\pi} q_{cgs}$

$\mathbf{E}_{LH} \ \stackrel{\mathrm{def}}{=}\ { \mathbf{E}_{cgs} \over \sqrt{4\pi} }$

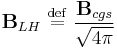$\mathbf{B}_{LH} \ \stackrel{\mathrm{def}}{=}\ { \mathbf{B}_{cgs} \over \sqrt{4\pi} }$ .

If additionally, the units are further defined so that c=1, then Maxwell and Lorentz equations become simply:

$\nabla \cdot \mathbf{E} = \rho \,$

$\nabla \cdot \mathbf{B} = 0 \,$

$\nabla \times \mathbf{E} = -\frac{ \partial \mathbf{B}} {\partial t} \,$

$\nabla \times \mathbf{B} = \frac{ \partial \mathbf{E}} {\partial t} %2B \mathbf{J} = \frac{ \partial \mathbf{E}} {\partial t} %2B \rho \mathbf{v} \,$

$\mathbf{F}_q = q \cdot (\mathbf{E} %2B \mathbf{v}_q \times \mathbf{B}) \,$

This demonstrates the simplicity that rationalizing the Lorentz–Heaviside units provide over equivalent unrationalized units. Note that there is no D flux density vector nor H magnetic field vector. With rationalized, natural LH units (with c=1) in free space, flux density is precisely the same quantity as electric field, D=E, and likewise, H=B describe the same magnetic field, thus unifying the concepts. There is no fundamental physical difference between the two. Additionally, if the magnetic interaction is understood as the electrostatic interaction with consideration of the effect of special relativity, it becomes clear that all electromagnetic interactions derive solely from electrostatic interaction.

References

^ ^a ^b Littlejohn, Robert (Fall 2007). "Gaussian, SI and Other Systems of Units in Electromagnetic Theory" (pdf). Physics 221A, University of California, Berkeley lecture notes. http://bohr.physics.berkeley.edu/classes/221/0708/notes/emunits.pdf. Retrieved 2008-05-06.
^ Kowalski, Ludwik, 1986, "A Short History of the SI Units in Electricity," The Physics Teacher 24(2): 97-99. Alternate web link (subscription required)

External links

Heaviside–Lorentz units

Systems of measurement

Metric systems	International System of Units · metre-kilogram-second · centimetre-gram-second · metre-tonne-second · gravitational system

Natural units	Geometric · Planck · Stoney · Lorentz–Heaviside · Atomic · Quantum chromodynamical

Conventional systems	Astronomical · Electrical · Temperature

Customary systems	Avoirdupois · Apothecaries' · British Imperial · Burmese · Canadian · Chinese · Cornish · Danish · Dutch · English · Finnish · French · German · Hindu · Hong Kong · Irish · Japanese · Maltese · Norwegian · Pegu · Polish · Portuguese · Romanian · Russian · Scottish · Spanish · Swedish · Taiwanese · Tatar · Turkish · Troy · United States

Ancient systems	Greek · Roman · Egyptian · Hebrew · Arabic · Mesopotamian · Persian · Indian

Other systems	Non-standard · Mesures usuelles · N-body