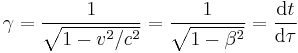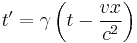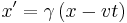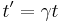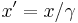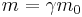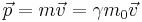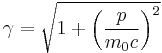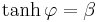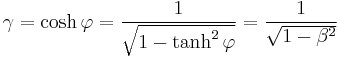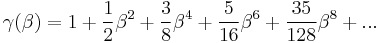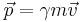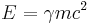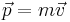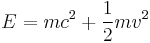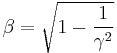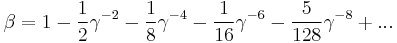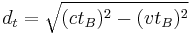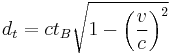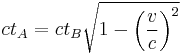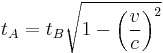Lorentz factor
The Lorentz factor or Lorentz term in special relativity is an expression which appears in several equations, including the time dilation, length contraction, and relativistic mass formulae, and the Lorentz transformations. The name originates from its earlier appearance in Lorentzian electrodynamics - named after the Dutch physicist Hendrik Lorentz.[1]
Due to its ubiquity, physicists generally represent it with the symbol γ (Greek lowercase gamma). Sometimes (especially in discussion of superluminal motion) the factor is written as Γ (Greek uppercase-gamma) rather than γ (lowercase-gamma).
Contents |
Definition
The Lorentz factor is defined as:[2]
where:
- v is the relative velocity between inertial reference frames,
- β is the ratio of v to the speed of light c (measured in m/s).
- τ is the proper time for an observer (measuring time intervals in the observer's own frame),
- c is the speed of light.
This is the most frequently used form in practice, though not the only one (see below for alternative forms).
Applications
Here is a list of formulae from Special relativity which include γ:[2][3]
- The Lorentz transforms: The simplest case is a boost in the x-direction (more general forms including arbitrary directions and rotations not listed here), which describe how space-time coordinates change from one inertial frame using coordinates (x, y, z, t) to another (x ', y ', z ', t '), in which the relative velocity is v:
- Corollaries of the above transformations are the results:
- Time dilation: An object moving with respect to an observer will be seen to move in slow motion, an elapsed time measured in the observer's frame t ' is related to the elapsed time in the objects frame t, where the factor is γ,
- Length contraction: The length of an object (along the direction of motion) with respect to an observer appears contracted, the measured length in the observer's frame is related to the length in the object's frame, the factor is 1/γ,
- Applying conservation of momentum and energy leads to these results:
- Relativistic mass: The mass of an object m in motion is dependant on γ and the rest mass m0,
- Relativistic momentum: The relativistic momentum relation takes the same form as for classical momentum, but using the above relativistic mass,
Numerical values
In the chart below, the left-hand column shows speeds as different fractions of the speed of light (i.e. in units of c). The middle column shows the corresponding Lorentz factor, the final is the reciprocal.
| Speed (units of c) | Lorentz factor | Reciprocal |
|---|---|---|
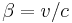 |
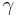 |
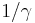 |
| 0.000 | 1.000 | 1.000 |
| 0.100 | 1.005 | 0.995 |
| 0.200 | 1.021 | 0.980 |
| 0.300 | 1.048 | 0.954 |
| 0.400 | 1.091 | 0.917 |
| 0.500 | 1.155 | 0.866 |
| 0.600 | 1.250 | 0.800 |
| 0.700 | 1.400 | 0.714 |
| 0.800 | 1.667 | 0.600 |
| 0.866 | 2.000 | 0.500 |
| 0.900 | 2.294 | 0.436 |
| 0.990 | 7.089 | 0.141 |
| 0.999 | 22.366 | 0.045 |
Alternative representations
Naturally there are other ways to write the factor. Above, velocity v was used, but related variables such as momentum and rapidity may also be convenient.
Momentum
Solving the previous relativistic momentum equation for γ leads to:
This form is rarely used, it does however appear in the Maxwell–Juttner distribution.[4]
Rapidity
Applying the definition of rapidity as the following hyperbolic angle φ:[5]
also leads to γ (by use of hyperbolic identities):
Using the property of Lorentz transformation, it can be shown that rapidity is additive, a useful property that velocity does not have. Thus the rapidity parameter forms a one-parameter group, a foundation for physical models.
Series expansion (velocity)
The Lorentz factor has a Maclaurin series of:
The approximation γ ≈ 1 + 1/2 β2 may be used to calculate relativistic effects at low speeds. It holds to within 1% error for v < 0.4 c (v < 120,000 km/s), and to within 0.1% error for v < 0.22 c (v < 66,000 km/s).
The truncated versions of this series also allow physicists to prove that special relativity reduces to Newtonian mechanics at low speeds. For example, in special relativity, the following two equations hold:
For γ ≈ 1 and γ ≈ 1 + 1/2 β2, respectively, these reduce to their Newtonian equivalents:
The Lorentz factor equation can also be inverted to yield:
This has an asymptotic form of:
The first two terms are occasionally used to quickly calculate velocities from large γ values. The approximation β ≈ 1 - 1/2 γ−2 holds to within 1% tolerance for γ > 2, and to within 0.1% tolerance for γ > 3.5.
Derivation
One of the fundamental postulates of Einstein's special theory of relativity is that all inertial observers will measure the same speed of light in vacuum regardless of their relative motion with respect to each other or the source. Imagine two observers: the first, observer  , traveling at a constant speed
, traveling at a constant speed  with respect to a second inertial reference frame in which observer
with respect to a second inertial reference frame in which observer  is stationary.
is stationary.  points a laser “upward” (perpendicular to the direction of travel). From
points a laser “upward” (perpendicular to the direction of travel). From  's perspective, the light is traveling at an angle. After a period of time
's perspective, the light is traveling at an angle. After a period of time 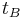 ,
,  has travelled (from
has travelled (from  's perspective) a distance
's perspective) a distance 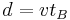 ; the light had travelled (also from
; the light had travelled (also from  perspective) a distance
perspective) a distance 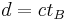 at an angle. The upward component of the path
at an angle. The upward component of the path  of the light can be solved by the Pythagorean theorem.
of the light can be solved by the Pythagorean theorem.
Factoring out 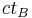 gives,
gives,
The distance that  sees the light travel is
sees the light travel is 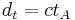 and equating this with
and equating this with  calculated from
calculated from  reference frame gives,
reference frame gives,
which simplifies to
See also
- Special relativity
- Inertial frame of reference
- Lorentz transformation
- Pseudorapidity
- Proper velocity
References
- ^ One universe, by Neil deGrasse Tyson, Charles Tsun-Chu Liu, and Robert Irion.
- ^ a b Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009, ISBN 978 0 470 01460 8
- ^ Sears' and Zemansky's University Physics, Young and Freedman (12th edition), Pearson Ed. & Addison-Wesley Inc., 2008, ISBN 978 0 321 50130 1
- ^ Synge, J.L (1957). The Relativistic Gas. Series in physics. North-Holland. LCCN 57-003567
- ^ Kinematics, by J.D. Jackson, See page 7 for definition of rapidity.