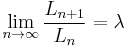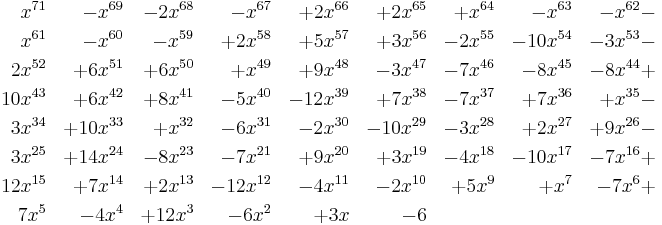Look-and-say sequence

In mathematics, the look-and-say sequence is the sequence of integers beginning as follows:

1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ... (sequence A005150 in OEIS).

To generate a member of the sequence from the previous member, read off the digits of the previous member, counting the number of digits in groups of the same digit. For example:

• 1 is read off as "one 1" or 11.
• 11 is read off as "two 1s" or 21.
• 21 is read off as "one 2, then one 1" or 1211.
• 1211 is read off as "one 1, then one 2, then two 1s" or 111221.
• 111221 is read off as "three 1s, then two 2s, then one 1" or 312211.

The idea is similar to that of run-length encoding.

If we start with any digit d from 0 to 9, d will remain indefinitely as the last digit of the sequence. For d different from 1, the sequence starts as follows:

d, 1d, 111d, 311d, 13211d, 111312211d, 31131122211d, …

Ilan Vardi has called this sequence, starting with d = 3, the Conway sequence (sequence A006715 in OEIS).^[1]

Basic properties

• The sequence grows indefinitely. In fact, any variant defined by starting with a different integer seed number will (eventually) also grow indefinitely, except for the degenerate sequence: 22, 22, 22, 22, …^[2].
• No digits other than 1, 2, and 3 appear in the sequence, unless the seed number contains such a digit or a run of more than three of the same digit.^[2]

• Conway's cosmological theorem: Every sequence eventually splits into a sequence of "atomic elements", which are finite subsequences that never again interact with their neighbors. There are 92 elements containing the digits 1, 2, and 3 only, which John Conway named after the natural chemical elements. There are also two "transuranic" elements for each digit other than 1,2, and 3.^[2][3]

• The terms eventually grow in length by about 30% per generation. If 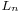denotes the number of digits of the 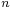-th member of the sequence, then the limit

where 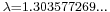is an algebraic number of degree 71^[2] known as Conway's constant. This fact was proven by Conway. This also holds for variants of the sequence starting with any integer other than 22.

Conway's constant is the unique positive real root of the following polynomial:

Origin

It was introduced and analyzed by John Conway in his paper "The Weird and Wonderful Chemistry of Audioactive Decay" published in Eureka 46, 5–18 in 1986.

Popularization

It is also popularly known as the Morris Number Sequence, after cryptographer Robert Morris, and the puzzle is sometimes referred to as the Cuckoo's Egg from a description of Morris in Clifford Stoll's book The Cuckoo's Egg.^[4][5]

Computer program

The following Python code generates a look-and-say sequence using lazy evaluation:

def look_and_say(member):
    while True:
        yield member
        breakpoints = [0]+[i for i in range(1,len(member)) if member[i-1] != member[i]]+[len(member)]
        groups = [member[breakpoints[i-1]:breakpoints[i]] for i in range(1,len(breakpoints))]
        member = ''.join(str(len(group)) + group[0] for group in groups)
 
# Print the 10-element sequence beginning with "1"
sequence = look_and_say("1")
for i in range(10):
    print sequence.next()

Pea pattern

This is described as being the series which counts the number of occurrences of a digit and appears for the first few steps to have similarities with the Look-andSay(1) series. Pea(1) proceeds 1, 11, 21, 1112 (reading as 1 occurence of 1 and 1 of 2), 3112, 211213, but after 15 steps Pea(1) loops at 21322314. This looping characteristic also occurs with Pea(2), Pea(3) and Pea(4). Pea(0) loops at 1021223314, with D=5-9 looping at 312233141D.

References

1. ^ Conway Sequence, MathWorld, accessed on line February 4, 2011.
2. ^ ^{a b c d} Martin, Oscar (2006). "Look-and-Say Biochemistry: Exponential RNA and Multistranded DNA". American mathematical monthly (Mathematical association of America) 113 (4): pp. 289–307. ISSN 0002-9890. http://www.uam.es/personal_pdi/ciencias/omartin/Biochem.PDF. Retrieved January 6, 2010. 
3. ^ Ekhad, S. B., Zeilberger, D.: Proof of Conway's lost cosmological theorem, Electronic Research Announcements of the American Mathematical Society, August 21, 1997, Vol. 5, pp. 78-82. Retrieved July 4, 2011.
4. ^ Robert Morris Sequence
5. ^ FAQ about Morris Number Sequence

External links

• Weisstein, Eric W., "Look and Say Sequence" from MathWorld.
• Look and Say sequence generator
• Sloane's A014715 : Decimal expansion of Conway's constant. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
• Look and Say sequence - from 0 up to 70 (very large)
• A Derivation of Conway’s Degree-71 “Look-and-Say” Polynomial