Log-normal distribution
| Probability density function |
|
| Cumulative distribution function |
|
| Notation | 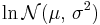 |
|---|---|
| Parameters | σ2 > 0 — shape (real), μ ∈ R — log-scale |
| Support | x ∈ (0, +∞) |
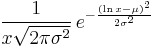 |
|
| CDF | ![\frac12 %2B \frac12\,\mathrm{erf}\Big[\frac{\ln x-\mu}{\sqrt{2\sigma^2}}\Big]](/2012-wikipedia_en_all_nopic_01_2012/I/1cf6e7a7ab84d8b95bb7400a2e295399.png) |
| Mean | 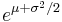 |
| Median | 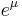 |
| Mode | 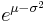 |
| Variance | 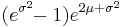 |
| Skewness | 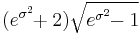 |
| Ex. kurtosis | 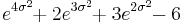 |
| Entropy | 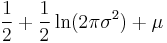 |
| MGF | (defined only on the negative half-axis, see text) |
| CF | representation 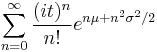 is asymptotically divergent but sufficient for numerical purposes is asymptotically divergent but sufficient for numerical purposes |
| Fisher information | 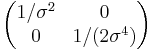 |
In probability theory, a log-normal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. If X is a random variable with a normal distribution, then Y = exp(X) has a log-normal distribution; likewise, if Y is log-normally distributed, then X = log(Y) is normally distributed. (This is true regardless of the base of the logarithmic function: if loga(Y) is normally distributed, then so is logb(Y), for any two positive numbers a, b ≠ 1.)
Log-normal is also written log normal or lognormal. It is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton.
A variable might be modeled as log-normal if it can be thought of as the multiplicative product of many independent random variables each of which is positive. For example, in finance, the variable could represent the compound return from a sequence of many trades (each expressed as its return + 1); or a long-term discount factor can be derived from the product of short-term discount factors. In wireless communication, the attenuation caused by shadowing or slow fading from random objects is often assumed to be log-normally distributed: see log-distance path loss model.
The log-normal distribution is the maximum entropy probability distribution for a random variate X for which the mean and variance of  is fixed. [1]
is fixed. [1]
Contents |
μ and σ
In a log-normal distribution, the parameters denoted μ and σ, are the mean and standard deviation, respectively, of the variable’s natural logarithm (by definition, the variable’s logarithm is normally distributed). On a non-logarithmized scale, μ and σ can be called the location parameter and the scale parameter, respectively.
In contrast, the mean and standard deviation of the non-logarithmized sample values are denoted m and s.d. in this article.
Characterization
Probability density function
The probability density function of a log-normal distribution is:
This follows by applying the change-of-variables rule on the density function of a normal distribution.
Cumulative distribution function
where erfc is the complementary error function, and Φ is the standard normal cdf.
Characteristic function and moment generating function
The characteristic function, E[e itX], has a number of representations. The integral itself converges for Im(t) ≤ 0. The simplest representation is obtained by Taylor expanding e itX and using formula for moments below, giving
This series representation is divergent for Re(σ2) > 0. However, it is sufficient for evaluating the characteristic function numerically at positive  as long as the upper limit in the sum above is kept bounded, n ≤ N, where
as long as the upper limit in the sum above is kept bounded, n ≤ N, where
and σ2 < 0.1. To bring the numerical values of parameters μ, σ into the domain where strong inequality holds true one could use the fact that if X is log-normally distributed then Xm is also log-normally distributed with parameters μm, σm. Since 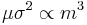 , the inequality could be satisfied for sufficiently small m. The sum of series first converges to the value of φ(t) with arbitrary high accuracy if m is small enough, and left part of the strong inequality is satisfied. If considerably larger number of terms are taken into account the sum eventually diverges when the right part of the strong inequality is no longer valid.
, the inequality could be satisfied for sufficiently small m. The sum of series first converges to the value of φ(t) with arbitrary high accuracy if m is small enough, and left part of the strong inequality is satisfied. If considerably larger number of terms are taken into account the sum eventually diverges when the right part of the strong inequality is no longer valid.
Another useful representation was derived by Roy Lepnik (see references by this author and by Daniel Dufresne below) by means of double Taylor expansion of e(ln x − μ)2/(2σ2).
The moment-generating function for the log-normal distribution does not exist on the domain R, but only exists on the half-interval (−∞, 0].
Properties
Location and scale
For the log-normal distribution, the location and scale properties of the distribution are more readily treated using the geometric mean and geometric standard deviation than the arithmetic mean and standard deviation.
Geometric moments
The geometric mean of the log-normal distribution is 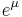 . Because the log of a log-normal variable is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median.[2]
. Because the log of a log-normal variable is symmetric and quantiles are preserved under monotonic transformations, the geometric mean of a log-normal distribution is equal to its median.[2]
The geometric mean (mg) can alternatively be derived from the arithmetic mean (ma) in a log-normal distribution by:
The geometric standard deviation is equal to 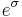 .
.
Arithmetic moments
If X is a lognormally distributed variable, its expected value (E - which can be assumed to represent the arithmetic mean), variance (Var), and standard deviation (s.d.) are
Equivalently, parameters μ and σ can be obtained if the expected value and variance are known:
For any real or complex number s, the sth moment of log-normal X is given by
A log-normal distribution is not uniquely determined by its moments E[Xk] for k ≥ 1, that is, there exists some other distribution with the same moments for all k. In fact, there is a whole family of distributions with the same moments as the log-normal distribution.
Mode and median
The mode is the point of global maximum of the probability density function. In particular, it solves the equation (ln ƒ)′ = 0:
The median is such a point where FX = 1/2:
Coefficient of variation
The coefficient of variation is the ratio s.d. over m (on the natural scale) and is equal to:
Partial expectation
The partial expectation of a random variable X with respect to a threshold k is defined as g(k) = E[X | X > k]P[X > k]. For a log-normal random variable the partial expectation is given by
This formula has applications in insurance and economics, it is used in solving the partial differential equation leading to the Black–Scholes formula.
Other
A set of data that arises from the log-normal distribution has a symmetric Lorenz curve (see also Lorenz asymmetry coefficient).[3]
Occurrence
- In biology, variables whose logarithms tend to have a normal distribution include:
- Measures of size of living tissue (length, height, skin area, weight);[4]
- The length of inert appendages (hair, claws, nails, teeth) of biological specimens, in the direction of growth;
- Certain physiological measurements, such as blood pressure of adult humans (after separation on male/female subpopulations).
- Subsequently, reference ranges for measurements in healthy individuals are more accurately estimated by assuming a log-normal distribution than by assuming a symmetric distribution about the mean.
- In hydrology, the log-normal distribution is used to analyze extreme values of such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.[5]
- The image on the right illustrates an example of fitting the log-normal distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.
- In finance, in particular the Black–Scholes model, changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal[6] (these variables behave like compound interest, not like simple interest, and so are multiplicative). However, some mathematicians such as Benoît Mandelbrot have argued that log-Levy distributions which possesses heavy tails would be a more appropriate model, in particular for the analysis for stock market crashes. Indeed stock price distribution typically exhibit a fat tail[7].
- The distribution of city sizes is lognormal. This follows from Gibrat's law of proportionate (or scale-free) growth. Irrespective of their size, all cities follow the same stochastic growth process. As a result, the logarithm of city size is normally distributed. There is also evidence of lognormality in the firm size distribution and of Gibrat's law.
- In reliability analysis, the lognormal distribution is often used to model times to repair a maintainable system.
- It has been proposed that coefficients of friction and wear may be treated as having a lognormal distribution [8]
Maximum likelihood estimation of parameters
For determining the maximum likelihood estimators of the log-normal distribution parameters μ and σ, we can use the same procedure as for the normal distribution. To avoid repetition, we observe that
where by ƒL we denote the probability density function of the log-normal distribution and by ƒN that of the normal distribution. Therefore, using the same indices to denote distributions, we can write the log-likelihood function thus:
Since the first term is constant with regard to μ and σ, both logarithmic likelihood functions, ℓL and ℓN, reach their maximum with the same μ and σ. Hence, using the formulas for the normal distribution maximum likelihood parameter estimators and the equality above, we deduce that for the log-normal distribution it holds that
Generating log-normally-distributed random variates
Given a random variate N drawn from the normal distribution with 0 mean and 1 standard deviation, then the variate
has a log-normal distribution with parameters  and
and  .
.
Related distributions
- If
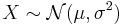 is a normal distribution, then
is a normal distribution, then 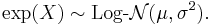
- If
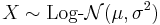 is distributed log-normally, then
is distributed log-normally, then 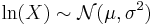 is a normal random variable.
is a normal random variable.
- If
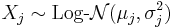 are n independent log-normally distributed variables, and
are n independent log-normally distributed variables, and 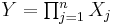 , then Y is also distributed log-normally:
, then Y is also distributed log-normally:
- Let
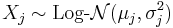 be independent log-normally distributed variables with possibly varying σ and μ parameters, and
be independent log-normally distributed variables with possibly varying σ and μ parameters, and 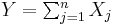 . The distribution of Y has no closed-form expression, but can be reasonably approximated by another log-normal distribution Z at the right tail. Its probability density function at the neighborhood of 0 is characterized in (Gao et al., 2009) and it does not resemble any log-normal distribution. A commonly used approximation (due to Fenton and Wilkinson) is obtained by matching the mean and variance:
. The distribution of Y has no closed-form expression, but can be reasonably approximated by another log-normal distribution Z at the right tail. Its probability density function at the neighborhood of 0 is characterized in (Gao et al., 2009) and it does not resemble any log-normal distribution. A commonly used approximation (due to Fenton and Wilkinson) is obtained by matching the mean and variance:
In the case that all 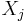 have the same variance parameter
have the same variance parameter 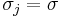 , these formulas simplify to
, these formulas simplify to
- If
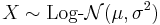 , then X + c is said to have a shifted log-normal distribution with support x ∈ (c, +∞). E[X + c] = E[X] + c, Var[X + c] = Var[X].
, then X + c is said to have a shifted log-normal distribution with support x ∈ (c, +∞). E[X + c] = E[X] + c, Var[X + c] = Var[X].
- If
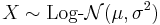 , then
, then 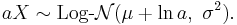
- If
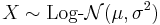 , then
, then 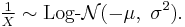
- If
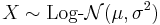 then
then 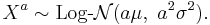 for
for 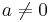
- Lognormal distribution is a special case of semi-bounded Johnson distribution
- If
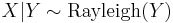 with
with 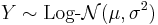 , then
, then 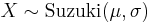 (Suzuki distribution)
(Suzuki distribution)
Similar distributions
- A substitute for the log-normal whose integral can be expressed in terms of more elementary functions (Swamee, 2002) can be obtained based on the logistic distribution to get the CDF
- This is a log-logistic distribution.
See also
- Error function
- Log-distance path loss model
- Slow fading
- Stochastic volatility
- Today's practical relevance: Nanoparticles
Notes
- ^ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model". Journal of Econometrics (Elsevier): 219–230. http://www.wise.xmu.edu.cn/Master/Download/..%5C..%5CUploadFiles%5Cpaper-masterdownload%5C2009519932327055475115776.pdf. Retrieved 2011-06-02.
- ^ Leslie E. Daly, Geoffrey Joseph Bourke (2000) Interpretation and uses of medical statistics Edition: 5. Wiley-Blackwell ISBN 0632047631, 9780632047635 (page 89)
- ^ Damgaard, Christian; Jacob Weiner (2000). "Describing inequality in plant size or fecundity". Ecology 81 (4): 1139–1142. doi:10.1890/0012-9658(2000)081[1139:DIIPSO]2.0.CO;2.
- ^ Huxley, Julian S. (1932). Problems of relative growth. London. ISBN 0486611140. OCLC 476909537.
- ^ Ritzema (ed.), H.P. (1994). Frequency and Regression Analysis. Chapter 6 in: Drainage Principles and Applications, Publication 16, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. pp. 175–224. ISBN 90 70754 3 39. http://www.waterlog.info/pdf/freqtxt.pdf.
- ^ Black, Fischer and Myron Scholes, "The Pricing of Options and Corporate Liabilities", Journal of Political Economy, Vol. 81, No. 3, (May/June 1973), pp. 637-654.
- ^ Bunchen, P., Advanced Option Pricing, University of Sydney coursebook, 2007
- ^ http://www.sciencedirect.com/science/article/pii/S0951832007002268
References
- Aitchison, J. and Brown, J.A.C. (1957) The Lognormal Distribution, Cambridge University Press.
- E. Limpert, W. Stahel and M. Abbt (2001) Log-normal Distributions across the Sciences: Keys and Clues, BioScience, 51 (5), 341–352.
- Eric W. Weisstein et al. Log Normal Distribution at MathWorld. Electronic document, retrieved October 26, 2006.
- Swamee, P.K. (2002). Near Lognormal Distribution, Journal of Hydrologic Engineering. 7 (6): 441–444
- Roy B. Leipnik (1991), On Lognormal Random Variables: I - The Characteristic Function, Journal of the Australian Mathematical Society Series B, vol. 32, pp 327–347.
- Gao et al. (2009), Asymptotic Behaviors of Tail Density for Sum of Correlated Lognormal Variables. International Journal of Mathematics and Mathematical Sciences.
- Daniel Dufresne (2009), SUMS OF LOGNORMALS, Centre for Actuarial Studies, University of Melbourne.
Further reading
- Robert Brooks, Jon Corson, and J. Donal Wales. "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion", in Advances in Futures and Options Research, volume 7, 1994.
|
|||||||||||
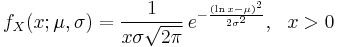
![F_X(x;\mu,\sigma) = \frac12 \operatorname{erfc}\!\left[-\frac{\ln x - \mu}{\sigma\sqrt{2}}\right] = \Phi\bigg(\frac{\ln x - \mu}{\sigma}\bigg),](/2012-wikipedia_en_all_nopic_01_2012/I/25ee238633094bde287f3085610b6b5f.png)
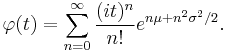
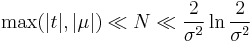
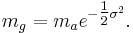
![\begin{align}
& \operatorname{E}[X] = e^{\mu %2B \tfrac{1}{2}\sigma^2}, \\
& \operatorname{Var}[X] = (e^{\sigma^2} - 1) e^{2\mu %2B \sigma^2} \\
& \operatorname{s.d.}[X] = \sqrt{\operatorname{Var}[X]} = e^{\mu %2B \tfrac{1}{2}\sigma^2}\sqrt{e^{\sigma^2} - 1} .
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/656dc62338980cd62fbd8cdbc80ba85e.png)
![\begin{align}
\mu &= \ln(\mathrm{E}[X]) - \frac12 \ln\!\left(1 %2B \frac{\mathrm{Var}[X]}{[\mathrm{E}[X]]^2}\right), \\
\sigma^2 &= \ln\!\left(1 %2B \frac{\mathrm{Var}[X]}{[\mathrm{E}[X]]^2}\right).
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/15de058a2b589fb9d8b45d1f6ccbf874.png)
![\operatorname{E}[X^s] = e^{s\mu %2B \tfrac{1}{2}s^2\sigma^2}.](/2012-wikipedia_en_all_nopic_01_2012/I/4beff9496b506b4f821644eb8cebd8bc.png)
![\mathrm{Mode}[X] = e^{\mu - \sigma^2}.](/2012-wikipedia_en_all_nopic_01_2012/I/cf8da3ba72bcc1f07730c021f6f895b6.png)
![\mathrm{Med}[X] = e^\mu\,.](/2012-wikipedia_en_all_nopic_01_2012/I/851eb4d1924fbec6d981f8c87d313adc.png)
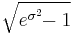
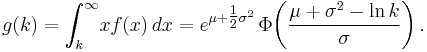
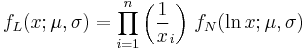
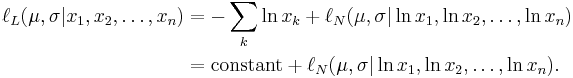
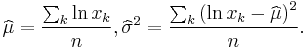
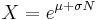
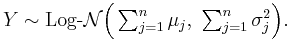
![\begin{align}
\sigma^2_Z &= \log\!\left[ \frac{\sum e^{2\mu_j%2B\sigma_j^2}(e^{\sigma_j^2}-1)}{(\sum e^{\mu_j%2B\sigma_j^2/2})^2} %2B 1\right], \\
\mu_Z &= \log\!\left[ \sum e^{\mu_j%2B\sigma_j^2/2} \right] - \frac{\sigma^2_Z}{2}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/4bd5c8f30e51a5ca067239fcd41cc872.png)
![\begin{align}
\sigma^2_Z &= \log\!\left[ (e^{\sigma^2}-1)\frac{\sum e^{2\mu_j}}{(\sum e^{\mu_j})^2} %2B 1\right], \\
\mu_Z &= \log\!\left[ \sum e^{\mu_j} \right] %2B \frac{\sigma^2}{2} - \frac{\sigma^2_Z}{2}.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/137d01f2288cd9e9e47ec16143a89170.png)
![F(x;\mu,\sigma) = \left[\left(\frac{e^\mu}{x}\right)^{\pi/(\sigma \sqrt{3})} %2B1\right]^{-1}.](/2012-wikipedia_en_all_nopic_01_2012/I/456274822de33ada09d28242305be392.png)