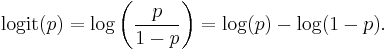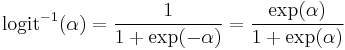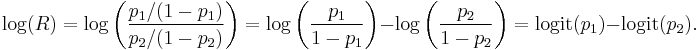Logit

This article discusses the binary logit function only. See discrete choice for a discussion of multinomial logit, conditional logit, nested logit, mixed logit, exploded logit, and ordered logit. For the basic regression technique that uses the logit function, see logistic regression.

The logit ( /ˈloʊdʒɪt/ loh-jit) function is the inverse of the sigmoidal "logistic" function used in mathematics, especially in statistics.

Log-odds and logit are synonyms^[1].

1 Definition
2 History
3 Uses and properties
4 See also
5 References
6 Further reading

Definition

The logit of a number p between 0 and 1 is given by the formula:

$\operatorname{logit}(p)=\log\left( \frac{p}{1-p} \right) =\log(p)-\log(1-p). \!\,$

The base of the logarithm function used is of little importance in the present article, as long as it is greater than 1, but the natural logarithm with base e is the one most often used.

The "logistic" function of any number $\alpha$ is given by the inverse-logit:

$\operatorname{logit}^{-1}(\alpha) = \frac{1}{1 %2B \operatorname{exp}(-\alpha)} = \frac{\operatorname{exp}(\alpha)}{1 %2B \operatorname{exp}(\alpha)}$

If p is a probability then p/(1 − p) is the corresponding odds, and the logit of the probability is the logarithm of the odds; similarly the difference between the logits of two probabilities is the logarithm of the odds ratio (R), thus providing a shorthand for writing the correct combination of odds ratios only by adding and subtracting:

$\operatorname{log}(R)=\log\left( \frac{{p_1}/(1-p_1)}{{p_2}/(1-p_2)} \right) =\log\left( \frac{p_1}{1-p_1} \right) - \log\left(\frac{p_2}{1-p_2}\right)=\operatorname{logit}(p_1)-\operatorname{logit}(p_2). \!\,$

History

The logit model was introduced by Joseph Berkson in 1944, who coined the term. The term was borrowed by analogy from the very similar probit model developed by Chester Ittner Bliss in 1934.^[2] G. A. Barnard in 1949 coined the commonly used term log-odds; the log-odds of an event is the logit of the probability of the event.

Uses and properties

The logit in logistic regression is a special case of a link function in a generalized linear model: it is the canonical link function for the binomial distribution.
The logit function is the negative of the derivative of the binary entropy function.
The logit is also central to the probabilistic Rasch model for measurement, which has applications in psychological and educational assessment, among other areas.
The inverse-logit function is also sometimes referred to as the expit function.^[3]

References

^ http://itl.nist.gov/div898/software/dataplot/refman2/auxillar/logoddra.htm
^ ^a ^b J. S. Cramer (2003). "The origins and development of the logit model". Cambridge UP. http://www.cambridge.org/resources/0521815886/1208_default.pdf.
^ http://www.stat.ucl.ac.be/ISdidactique/Rhelp/library/msm/html/expit.html

Logit

Contents

Definition

History

Uses and properties

See also

References

Further reading