Locally decodable code
A locally decodable code is an error-correcting code that allows to decode a single bit of a message with high probability by only looking at a small number of bits of a possibly partially corrupted codeword.[1][2] The related locally testable codes merely require that it can be locally detected whether a given message is close to a codeword, and in this sense locally decodable codes are a special case of locally testable codes.
More formally, a  -query locally decodable code encodes an
-query locally decodable code encodes an  -bit message
-bit message  by an
by an  -bit codeword
-bit codeword 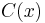 such that any bit
such that any bit  of the message can be probabilistically recovered by querying only
of the message can be probabilistically recovered by querying only  bits of the codeword
bits of the codeword 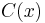 , even if some constant fraction of the codeword has been corrupted.
, even if some constant fraction of the codeword has been corrupted.
Examples
The Walsh–Hadamard code 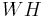 is a simple, locally decodable code. It has an optimal
is a simple, locally decodable code. It has an optimal 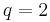 queries and a best possible decoding error. However, codewords of
queries and a best possible decoding error. However, codewords of  -bit messages have exponential length
-bit messages have exponential length 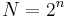 , which is why the Walsh–Hadamard code has a very inefficient rate. If a received signal
, which is why the Walsh–Hadamard code has a very inefficient rate. If a received signal 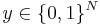 agrees with some codeword
agrees with some codeword 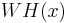 for some message
for some message 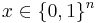 on at least a
on at least a 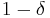 fraction of bits, then
fraction of bits, then  can be recovered from
can be recovered from  with probability
with probability 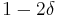 .[3]
.[3]
References
- ^ Rafail Ostrovsky, Omkant Pandey, Amit Sahai. "Private Locally Decodable Codes". http://eprint.iacr.org/2007/025.pdf.
- ^ Sergey Yekhanin. New locally decodable codes and private information retrieval schemes, Technical Report ECCC TR06-127, 2006.
- ^ Section 11.5.2 of Arora, Sanjeev; Barak, Boaz (2009). Computational Complexity: A Modern Approach. Cambridge. ISBN 978-0-521-42426-4. http://www.cs.princeton.edu/theory/complexity/