List of aperiodic sets of tiles

In geometry, a tiling is a family of shapes – called tiles – that cover the plane (or any other geometric setting) without gaps or overlaps.[1] Such a tiling might be constructible from a single fundamental unit or primitive cell and is then called periodic.[2] An example of such a tiling is shown in the diagram to the right (see the image description for more information). Every periodic tiling has a primitive cell that can generate it. A tiling that cannot be constructed from a single primitive cell is called nonperiodic. If a given set of tiles allows only nonperiodic tilings, then this set of tiles is called aperiodic.[3] The tilings obtained from an aperiodic set of tiles can be called aperiodic tilings.

The first table explains the abbreviations used in the second table. The second table contains all known aperiodic sets of tiles and gives some additional basic information about each set. Please note that this list of tiles is still incomplete.

Contents

Explanations

Abbreviation Meaning Explanation
E2 Euclidean plane normal flat plane
H2 hyperbolic plane plane, where the parallel postulate does not hold
E3 Euclidean 3 space space defined by three perpendicular coordinate axes
MLD Mutually locally derivable two tilings are said to be mutually locally derivable from each other, if one tiling can be obtained from the other by a simple local rule (such as deleting or inserting an edge)

List

Image Name Number of tiles Space Publication Date refs Comments
Trilobite and cross tiles 2 E2 1999 [4] Tilings MLD from the chair tilings
Penrose P1 tiles 6 E2 1974[Note 1] [5] Tilings MLD from the tilings by P2 and P3, Robinson triangles, and "Starfish, ivy leaf, hex"
Penrose P2 tiles 2 E2 1977[Note 2] [6] Tilings MLD from the tilings by P1 and P3, Robinson triangles, and "Starfish, ivy leaf, hex"
Penrose P3 tiles 2 E2 1978[Note 3] [7] Tilings MLD from the tilings by P1 and P2, Robinson triangles, and "Starfish, ivy leaf, hex"
Binary tiles 2 E2 1988 [8][9] Although similar in shape to the P3 tiles, the tilings are not MLD from each other, developed in an attempt to model the atomic arrangement in binary alloys
Robinson tiles 6 E2 1971[Note 4] [10] Tiles enforce aperiodicity by forming an infinite hierarchy of square lattices
No image Ammann A1 tiles 6 E2 1977[11] [12] Tiles enforce aperiodicity by forming an infinite hierarchal binary tree.
Ammann A2 tiles 2 E2 1986[Note 5] [13]
Ammann A3 tiles 3 E2 1986[Note 5] [13]
Ammann A4 tiles 2 E2 1986[Note 5] [13][14] Tilings MLD with Ammann A5.
Ammann A5 tiles 2 E2 1982[Note 6] [15][16] Tilings MLD with Ammann A4.
No image Penrose Hexagon-Triangle tiles 2 E2 1997[17] [17][18]
No image Golden Triangle tiles 10 E2 2001 [19] [20] date is for discovery of matching rules. Dual to Ammann A2
Socolar tiles 3 E2 1989[Note 7] [21][22] Tilings MLD from the tilings by the Shield tiles
Shield tiles 4 E2 1988[Note 8] [23][24] Tilings MLD from the tilings by the Socolar tiles
Square triangle tiles 5 E2 1986[25] [26]
No image Sphinx tiles 91 E2 [27]
Starfish, ivy leaf and hex tiles 3 E2 [28][29][30] Tiling is MLD to Penrose P1, P2, P3, and Robinson triangles
Robinson triangle 4 E2 [12] Tiling is MLD to Penrose P1, P2, P3, and "Starfish, ivy leaf, hex".
Danzer triangles 6 E2 1996[31] [32]
Pinwheel tiles E2 1994[33][34] [35][36] Date is for publication of matching rules.
No image Wang tiles 104 E2 2008[Note O] [37]
No image Wang tiles 56 E2 1971[Note 4] [38] Tiles enforce aperiodicity by forming an infinite hierarchy of square lattices
Wang tiles 32 E2 [39]
Wang tiles 16 E2 [40][41]
Wang tiles 14 E2 [42]
Wang tiles 13 E2 1996 [43][44]
No image Decagonal Sponge tile 1 E2 2002 [45][46] Porous tile consisting of non-overlapping point sets
No image Horocyclic tiles 85 H2 2005 [47]
Goodman-Strauss hyperbolic tile 1 H2 2005 [48] Weakly aperiodic
No image Goodman-Strauss strongly aperiodic tiles 26 H2 2005 [48]
No image Böröczky tile 1 Hn 1974[49] [50] Not strongly aperiodic
No image Schmitt tile 1 E3 1988 [51] Screw-periodic
Schmitt-Conway-Danzer tile 1 E3 [51] Screw-periodic and convex
Socolar Taylor tile 1 E3 2010 [52][53] Periodic in third dimension
No image Penrose rhombohedra 2 E3 1981[54] [55][56][57][58][59][60][61]
No image Wang cubes 21 E3 [62]
No image Wang cubes 18 E3 [63]
No image Wang cubes 16 E3 [64]
No image Danzer tetrahedra 4 E3 1989[65] [66]
I and L tiles 2 En for all n ≥ 3 1999 [67]

Notes

First published in

1.^ Penrose, R. (1974), "The role of Aesthetics in Pure and Applied Mathematical Research", Bull. Inst. Math. and its Appl. 10: 266-271
2.^ Gardner, M. (January 1977), "Extraordinary nonperiodic tiling that enriches the theory of tiles", Scientific American 236: 110-121
3.^ Penrose, R. (1978), "Pentaplexity", Eureka 39: 16-22
4.^ Robinson, R. (1971), "Undecidability and nonperiodicity of tilings in the plane", Inv. Math. 12: 177-209
5.^ Grünbaum, B.; Shephard, G. C. (1986), Tilings and Patterns, New York: W. H. Freeman, ISBN 0-7167-1194-X .
6.^ Beenker, F. P. M.(1982), "Algebraic theory of non-periodic tilings of the plane by two simple building blocks: a square and a rhombus", Eindhoven University of Technology, TH Report 82-WSK04
7.^ Socolar, J. E. S. (1989), "Simple octagonal and dodecagonal quasicrystals", Phys. Rev. A 39: 10519-51
8.^ Gähler, F., "Crystallography of dodecagonal quasicrystals", published in Janot, C.: Quasicrystalline materials : Proceedings of the I.L.L. / Codest Workshop, Grenoble, 21–25 March 1988. Singapore : World Scientific, 1988, 272-284

References

  1. ^ Grünbaum B., Shephard G. C. (1977), "Tilings by Regular Polygons", Math. Mag. 50 (5): 227–247, doi:10.2307/2689529, http://vohweb.chem.ucla.edu/voh/classes%5Cspring10%5CM117%20HNRS%20M180ID22%5CGrunbaumShephardTilingByRegPolygons.pdf. (archived at WebCite)
  2. ^ Edwards S., Fundamental Regions and Primitive cells (archived at WebCite)
  3. ^ Ollinger N. Mathematica in action (see page 268)
  4. ^ Goodman-Strauss C. (1999), "A Small Aperiodic Set of Planar Tiles", European J. Combinatorics 20 (5): 375–384, doi:10.1006/eujc.1998.0281  (preprint available here)
  5. ^ Mikhael J. Colloidal Monolayers On Quasiperiodic Laser Fields (see page 23) (archived at WebCite)
  6. ^ Gardner M. Penrose tiles to trapdoor ciphers (see page 86) (archived at WebCite)
  7. ^ Penrose R. (1979/80), "Pentaplexity", Math. Intell. 2: 32–37, http://www.ma.utexas.edu/users/radin/pentaplexity.html. (archived at WebCite)
  8. ^ Lançon F., Billard L. (1988), "Two-dimensional system with a quasi-crystalline ground state", J. Phys. France 49 (2): 249–256, doi:10.1051/jphys:01988004902024900, http://hal.archives-ouvertes.fr/docs/00/21/06/91/PDF/ajp-jphys_1988_49_2_249_0.pdf.  (archived at WebCite)
  9. ^ Lançon F., Billard L. (1992), "A simple example of a non-Pisot tiling with five-fold symmetry", J. Phys. I France 2 (2): 207–220, doi:10.1051/jp1:1992134, http://hal.archives-ouvertes.fr/docs/00/24/64/73/PDF/ajp-jp1v2p207.pdf. (archived at WebCite)
  10. ^ Goodman-Strauss C. (1999), "Aperiodic Hierarchical tilings", Proc. of NATO-ASI "Foams, Emulsions, and Cellular Materials" Ser. E 354: 481–496, http://www.webcitation.org/5sxslGkXb. 
  11. ^ Gardner, Martin (2001). The Colossal Book of Mathematics. W. W. Norton & Company. p. 76. 
  12. ^ a b Grünbaum B. and Shephard G. C.. Tilings and Patterns. , according to [1]; cf [2]
  13. ^ a b c Ammann R., Grünbaum B. and Shephard G. C. (1992), "Aperiodic Tiles", Discrete Comp Geom 8: 1–25, doi:10.1007/BF02293033, http://www.webcitation.org/5rjblcapr. 
  14. ^ Harris E., Frettlöh D. Ammann A4
  15. ^ Komatsu K., Nomakuchi K., Sakamoto K., Tokitou T. (2004), "Representation of Ammann-Beenker tilings by an automaton", Nihonkai Math. J. 15: 109–118, http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.nihmj/1273779794. (archived at WebCite)
  16. ^ Harris E., Frettlöh D. Ammann-Beenker
  17. ^ a b Penrose R. (1997), "Remarks on tiling: Details of a (1+ε+ε2) aperiodic set.", Nato Asi Series C 489 The Mathematics of Long-Range Aperiodic Order: 467–497, ISBN 9780792345060, http://books.google.com/?id=3YGXr_nQFw8C&printsec=frontcover&dq=quasicrystals+and+geometry#v=onepage&q=quasicrystals%20and%20geometry&f=false. 
  18. ^ Goodman-Strauss C., An aperiodic pair of tiles
  19. ^ Danzer, Ludwig; van Ophuysen, Gerrit (2001). "A species of planar triangular tilings with inflation factor 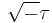\sqrt-\tau". Res. Bull. Panjab Univ. Sci. 50 (1-4): 137–175. doi:2003f:52015. 
  20. ^ Gelbrich, G (1997). "Fractal Penrose tiles II. Tiles with fractal boundary as duals of Penrose triangles". Aequationes Math. 54: 108–116. MRMR1466298. 
  21. ^ Gähler F., Lück R., Ben-Abraham S. I., Gummelt P.Dodecagonal tilings as maximal cluster coverings (archived at WebCite)
  22. ^ The Socolar tiling
  23. ^ Gähler F., Frettlöh D. Shield
  24. ^ Gähler F. (1993), "Matching rules for quasicrystals: the composition-decomposition method", J. of Non-crystalline Solids 153&154: 160–164, http://elib.uni-stuttgart.de/opus/volltexte/2009/3989/pdf/gaeh11.pdf. (archived at WebCite)
  25. ^ Stampfli, P (1986). "A Dodecagonal Quasiperiodic Lattice in Two Dimensions". Helv. Phys. Acta. 59: 1260–1263. 
  26. ^ Hermisson J., Richard C., Baake M. A Guide to the Symmetry Structure of Quasiperiodic Tiling Classes (archived at WebCite)
  27. ^ Goodman-Strauss C., Aperiodic tilings (see page 74)
  28. ^ Lord E. A. (1991), "Quasicrystals and Penrose patterns", Current Science 61: 315, http://www.webcitation.org/5t3XY5gd3. 
  29. ^ Olamy Z., Kléman M. (1989), "A two dimensional aperiodic dense tiling", J. Phys. France 50: 19–33, doi:10.1051/jphys:0198900500101900, http://hal.archives-ouvertes.fr/docs/00/21/08/96/PDF/ajp-jphys_1989_50_1_19_0.pdf.  (archived at WebCite)
  30. ^ Mihalkovič M., Henley C. L., Widom M. (2004), "Combined energy-diffraction data refinement of decagonal AlNiCo", J. Non-Cryst. Solids 334&335: 177–183, http://people.ccmr.cornell.edu/~clh/PUBS/dfit-04.pdf.  (archived at WebCite)
  31. ^ Nischke, K-P and Danzer, L, "A construction of inflation rules based on $n$-fold symmetry". Discrete Comput. Geom. 15 (2): 221–236. 1996.  96j:52035
  32. ^ Hayashi H., Kawachi Y., Komatsu K., Konda A., Kurozoe M., Nakano F., Odawara N., Onda R., Sugio A., Yamauchi M. Abstract:Notes on vertex atlas of planar Danzer tiling
  33. ^ Radin, C (1994). "The pinwheel tilings of the plane". Annals of Mathematics(2) 139 (3): 661–702. doi:10.2307/2118575. JSTOR 2118575. MR95d:52021. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.44.9723&rank=1. Retrieved 2010-04-03. 
  34. ^ Charles Radin (1994). "Symmetry Of Tilings Of The Plane". Annals of Math. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.45.5319&rank=6. Retrieved 2010-04-03. 
  35. ^ Radin, C; Wolff, M (1992). "Space tilings and local isomorphism". Geom. Dedicata 42 (3): 355–360. MR1164542. 
  36. ^ Radin, C (1997). "Aperiodic tilings, ergodic theory, and rotations". The mathematics of long-range aperiodic order. Kluwer Acad. Publ., Dordrecht. MR1460035. 
  37. ^ Ollinger N. Two-by-two Substitution systems and the Undecidability of the Domino Problem (see pages 476-485)
  38. ^ Kari, J.; Papasoglu, P. (1999). "Deterministic Aperiodic Tile Sets". Geometric and Functional Analysis 9: 353–369. 
  39. ^ Lagae A., Kari J., Dutré P. (2006), "Aperiodic Sets of Square Tiles with Colored Corners", Report CW 460: 12, http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=9F2387ADDE287538436CC970669B4ABC?doi=10.1.1.89.1294&rep=rep1&type=pdf. (archived at WebCite)
  40. ^ Grünbaum, B.; Shephard, G. C. (1986), Tilings and Patterns, New York: W. H. Freeman, ISBN 0-7167-1194-X 
  41. ^ Carbone, A.; Gromov, M.; Prusinkiewicz, P. (2000), Pattern Formation in Biology, Vision and Dynamics, Singapore: World Scientific Publishing Co. Pte. Ltd., ISBN 9810237928 
  42. ^ Lagae A. Tile Based Methods in Computer Graphics Dissertation (see page 149) (archived at WebCite)
  43. ^ Culik K., Kari J. On aperiodic sets of Wang tiles
  44. ^ Culik K. An aperiodic set of 13 Wang tiles (archived at WebCite)
  45. ^ Zhu F. The Search for a Universal Tile
  46. ^ Bailey D. A., Zhu F. A Sponge-Like (Almost) Universal Tile
  47. ^ Goodman-Strauss C., A hierarchical strongly aperiodic set of tiles in the hyperbolic plane
  48. ^ a b Goodman-Strauss C. (2005), "A strongly aperiodic set of tiles in the hyperbolic plane", Invent. Math. 159: 120, Bibcode 2004InMat.159..119G, doi:10.1007/s00222-004-0384-1 
  49. ^ Böröczky, K. (1974), "Gömbkitöltések állandó görbületü terekben I", Mat. Lapok. 25: 265–306. Böröczky, K. (1974), "Gömbkitöltések állandó görbületü terekben II", Mat. Lapok. 26: 67–90. 
  50. ^ Dolbilin N., Frettlöh D. Properties of Böröczky tilings in high dimensional hyperbolic spaces (archived at WebCite)
  51. ^ a b Radin, Charles (1995), "Aperiodic tilings in higher dimensions" (fee required), Proceedings of the American Mathematical Society (American Mathematical Society) 123 (11): 3543–3548, doi:10.2307/2161105, JSTOR 2161105. 
  52. ^ Socolar J. E. S. and Taylor J. M. An aperiodic hexagonal tile
  53. ^ Socolar J. E. S. and Taylor J. M. Forcing nonperiodicity with a single tile
  54. ^ Mackay A. L. (1981), "De Nive Quinquangula: On the pentagonal snowflake", Sov. Phys. Crystallogr. 26(5): 517–522, http://materials.iisc.ernet.in/~lord/webfiles/Alan/CV073eng.pdf.  (archived at WebCite)
  55. ^ Meisterernst G. Experimente zur Wachstumskinetik Dekagonaler Quasikristalle (Experiments on the growth kinetics of decagonal quasicrystals) Dissertation (see page 18-19) (archived at WebCite)
  56. ^ Jirong S. (1993), "Structure Transition of the Three-Dimensional Penrose Tiling Under Phason Strain Field", Chinese Phys. Lett. 10, No.8: 449–452, http://cpl.iphy.ac.cn/qikan/manage/wenzhang/0100449.pdf.  (archived at WebCite)
  57. ^ Inchbald G. A 3-D Quasicrystal Structure
  58. ^ Lord E. A., Ranganathan S., Kulkarni U. D. (2001), "Quasicrystals: tiling versus clustering", Phil. Mag. A 81: 2645–2651, http://materials.iisc.ernet.in/~lord/webfiles/pmq.pdf.  (archived at WebCite)
  59. ^ Rudhart C. P. Zur numerischen Simulation des Bruchs von Quasikristallen (On the numeric simulation of cracking in quasicrystals) see page 11
  60. ^ Lord E. A., Ranganathan S., Kulkarni U. D. (2000), "Tilings, coverings, clusters and quasicrystals", Current Science 78, No.1: 64–72, http://materials.iisc.ernet.in/~lord/webfiles/eric/pdfs/55.pdf.  (archived at WebCite)
  61. ^ Katz A. (1988), "Theory of Matching Rules for the 3-Dimensional Penrose Tilings", Commun. Math. Phys. 118 (2): 263–288, doi:10.1007/BF01218580, http://projecteuclid.org/DPubS/Repository/1.0/Disseminate?view=body&id=pdf_1&handle=euclid.cmp/1104161989.  (archived at WebCite)
  62. ^ Culik K., Kari J. An aperiodic set of Wang cubes
  63. ^ Walther, G.; Selter, C. (1999), Mathematikdidaktik als design science, Leipzig: Ernst Klett Grundschulverlag, ISBN 3-12-2000060-1 
  64. ^ Lu A., Ebert D. S., Qiao W., Kraus M., Mora B. Interactive volume illustration using Wang cubes
  65. ^ Danzer, L. (1989), "Three-Dimensional Analogs of the Planar Penrose Tilings and Quasicrystals.", Discrete Mathematics 76: 1–7, doi:10.1016/0012-365X(89)90282-3 
  66. ^ Zerhusen A., Danzer's three dimensional tiling
  67. ^ Goodman-Strauss C. (1999), "An Aperiodic Pair of Tiles in En for all n ≥ 3", Europ. J. Combinatorics 20 (5): 385–395, doi:10.1006/eujc.1998.0282  (preprint available here)

External links