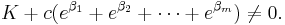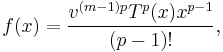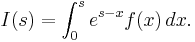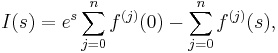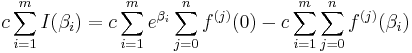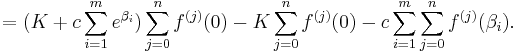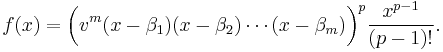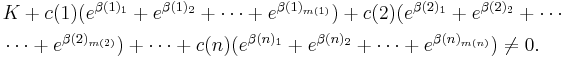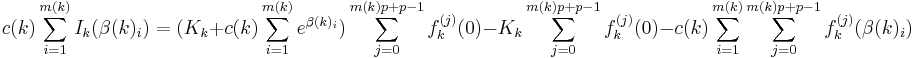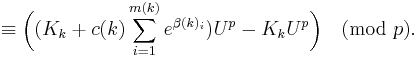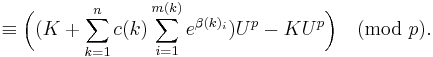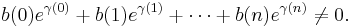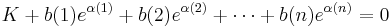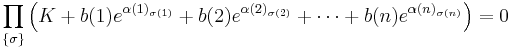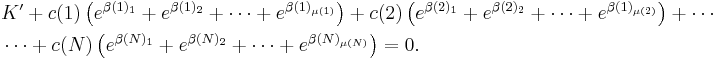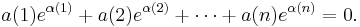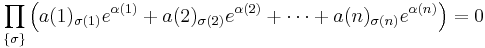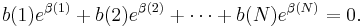LindemannâWeierstrass theorem

the mathematical constant $Ï$
Part of a series of articles on

Uses
Area of disk Circumference Use in other formulae
Properties
Irrationality Transcendence Less than 22/7
Value
Approximations Memorization
People
Archimedes Liu Hui Zu Chongzhi Madhava of Sangamagrama William Jones John Machin John Wrench Ludolph van Ceulen Aryabhata
History
Chronology Book
In culture
Legislation Holiday
Related topics
Squaring the circle Basel problem Tau ( $Ï$ ) Other topics related to $Ï$

Part of a series of articles on
The mathematical constant $e$

Natural logarithm Â· Exponential function

Applications in: compound interest Â· Euler's identity & Euler's formula Â· half-lives & exponential growth/decay

Defining $e$ : proof that $e$ is irrational Â· representations of $e$ Â· LindemannâWeierstrass theorem

People John Napier Â· Leonhard Euler

Schanuel's conjecture

In mathematics, the LindemannâWeierstrass theorem is a result that is very useful in establishing the transcendence of numbers. It states that if $Î\pm$ ₁, ..., $Î\pm$ _$n$ are algebraic numbers which are linearly independent over the rational numbers $Q$ , then $e$ ^{$Î\pm$ ₁}, ..., $e$ ^{$Î\pm$ _$n$} are algebraically independent over Q; in other words the extension field $Q$ ( $e$ ^{$Î\pm$ ₁}, ..., $e$ ^{$Î\pm$ _$n$}) has transcendence degree $n$ over $Q$ .

An equivalent formulation (Baker 1975, Chapter 1, Theorem 1.4), is the following: If $Î\pm$ ₁, ..., $Î\pm$ _$n$ are distinct algebraic numbers, then the exponentials $e$ ^Î±₁, ..., $e$ ^{$Î\pm$ _$n$} are linearly independent over the algebraic numbers. This equivalence transforms a linear relation over the algebraic numbers into an algebraic relation over the rational numbers by using the fact that a symmetric polynomial whose arguments are all conjugates of one another gives a rational number.

The theorem is named for Ferdinand von Lindemann and Karl Weierstrass. Lindemann proved in 1882 that $e$ ^$Î\pm$ is transcendental for every non-zero algebraic number $Î\pm$ , thereby establishing that pi ( $Ï$ ) is transcendental (see below). Weierstrass proved the above more general statement in 1885.

The theorem, along with the GelfondâSchneider theorem, is generalized by Schanuel's conjecture.

1 Naming convention
2 Transcendence of e and Ï
3 p-adic conjecture
4 Modular conjecture
5 A proof sketch
6 References
7 Further reading

Naming convention

The theorem is also known variously as the HermiteâLindemann theorem and the HermiteâLindemannâWeierstrass theorem. Charles Hermite first proved the simpler theorem where the $Î\pm$ _$i$ exponents are required to be rational integers and linear independence is only assured over the rational integers,^[1] a result sometimes referred to as Hermite's theorem.^[2] Although apparently a rather special case of the above theorem, the general result can be reduced to this simpler case. Lindemann was the first to allow algebraic numbers into Hermite's work in 1882.^[3] Shortly afterwards Weierstrass obtained the full result,^[4] and further simplifications have been made by several mathematicians, most notably by David Hilbert.

Transcendence of $e$ and $Ï$

The transcendence of $e$ and $Ï$ are direct corollaries of this theorem.

Suppose $Î\pm$ is a nonzero algebraic number; then $Î\pm$ is a linearly independent set over the rationals, and therefore by the first formulation of the theorem { $e$ ^$Î\pm$} is an algebraically independent set; or in other words $e$ ^$Î\pm$ is transcendental. In particular, $e$ ¹ = $e$ is transcendental. (A more elementary proof that $e$ is transcendental is outlined in the article on transcendental numbers.)

Alternatively, by the second formulation of the theorem, if $Î\pm$ is a nonzero algebraic number, then {0, $Î\pm$ } is a set of distinct algebraic numbers, and so the set { $e$ ⁰, $e$ ^$Î\pm$} = {1, $e$ ^$Î\pm$} is linearly independent over the algebraic numbers and in particular $e$ ^$Î\pm$ cannot be algebraic and so it is transcendental.

The proof that $Ï$ is transcendental is by contradiction. If $Ï$ were algebraic, $Ï$ $i$ would be algebraic as well, and then by the LindemannâWeierstrass theorem $e$ ^{$Ï$ $i$} = â1 (see Euler's identity) would be transcendental, a contradiction.

A slight variant on the same proof will show that if $Î\pm$ is a nonzero algebraic number then sin( $Î\pm$ ), cos( $Î\pm$ ), tan( $Î\pm$ ) and their hyperbolic counterparts are also transcendental.

$p$ -adic conjecture

The $p$ -adic LindemannâWeierstrass conjecture is that a $p$ -adic analog of this statement is also true: Suppose $p$ is some prime number and $Î\pm$ ₁, ..., $Î\pm$ _$n$ are $p$ -adic numbers which are algebraic over $Q$ and linearly independent over $Q$ , such that | $Î\pm$ _$i$|_$p$ < 1/ $p$ for all $i$ ; then the $p$ -adic exponentials exp_$p$( $Î\pm$ ₁), ..., $exp$ _$p$( $Î\pm$ _$n$) are $p$ -adic numbers that are algebraically independent over $Q$ .

Modular conjecture

An analogue of the theorem involving the modular function j was conjectured by Daniel Bertrand in 1997, and remains an open problem.^[5] Writing q = e^{2Ïi $Ï$} for the nome and j( $Ï$ ) = J(q), the conjecture is as follows. Let q₁,â¦,q_n be non-zero algebraic numbers in the complex unit disc such that the 3n numbers J(q_i), J^â²(q_i), J^â²â²(q_i) (1 â¤ i â¤ n) are algebraically dependent over the rational numbers. Then there exist two indices 1 â¤ i < j â¤ n such that q_i and q_j are multiplicatively dependent.

A proof sketch

We prove Baker's reformulation of the theorem: that if $a$ ₁, $a$ ₂... $a$ _$n$ are non-zero algebraic numbers, and $Î\pm$ ₁, $Î\pm$ ₂... $Î\pm$ _$n$ are distinct algebraic numbers, then 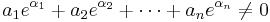$a_1 e^{\alpha_1} %2B a_2 e^{\alpha_2} %2B\cdots %2B a_n e^{\alpha_n}\ne 0$ .^[6]

Lemma A

If $K$ and $c$ are non-zero integers, and $Î²$ ₁ ... $Î²$ _$m$ are the roots of a polynomial with integer coefficients $T$ ( $x$ ) $=$ $v x$ ^$m$ + ... + $u$ , and $v$ , $u$ â 0, then

$K%2Bc(e^{\beta_1} %2B e^{\beta_2} %2B\cdots %2B e^{\beta_m}) \ne 0. \,$

Before proving the lemma, let us look at the following function:

$f(x) = \frac {v^{(m-1)p} T^p(x) x^{p-1}}{(p-1)!},$

where $p$ is a prime number, and at the integral:

$I(s) = \int^s_0 e^{s-x} f(x) \, dx.$

(Up to a factor, this is the same integral appearing in the proof that $e$ is a transcendental number, where $Î²$ ₁, $Î²$ ₂, ..., $Î²$ _$m$ $=$ 1, 2, ..., $m$ . The rest of the proof of the Lemma is analog to that proof.)

It can be shown by integration by parts that

$I(s) = e^s \sum_{j=0}^n f^{(j)}(0) - \sum_{j=0}^n f^{(j)}(s),$

where $n$ = $mp$ + $p$ â 1 is the degree of $f$ , and $f$ ^{( $j$ )} is the $j$ -th derivative of $f$ .

Let us consider the following sum:

$c\sum_{i=1}^m I(\beta_i) = c\sum_{i=1}^m e^{\beta_i} \sum_{j=0}^n f^{(j)}(0) - c \sum_{i=1}^m \sum_{j=0}^n f^{(j)}(\beta_i)$

$= (K%2B c\sum_{i=1}^m e^{\beta_i}) \sum_{j=0}^n f^{(j)}(0) - K \sum_{j=0}^n f^{(j)}(0) - c\sum_{i=1}^m \sum_{j=0}^n f^{(j)}(\beta_i).$

We will show that the term at the left approaches zero as $p$ goes to infinity, while the last two terms at the right sum up to a non-zero integer for a large enough $p$ . Additionally, the term multiplying the parentheses is a non-zero integer for large enough $p$ . Thus, the term inside the parentheses cannot vanish, and the Lemma will be proven.

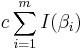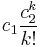$c \sum_{i=1}^m I(\beta_i)$ can be shown to approach zero as $p â â$ by noting that: $|{I(s)}| \le |s|\cdot\max_{x\in [0,s]}[|T(x)|]\cdot \frac{(\max_{x\in [0,s]}[|xT(x)|])^{(p-1)}}{(p-1)!}$ , which for a given s has the form $c_1 \frac{c_2^k}{k!}$ with $c$ ₁, $c$ ₂ constants and $k$ = $p$ â 1. This goes to zero as $k$ goes to infinity.

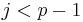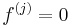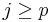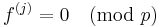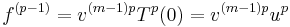It follows from the definition of $f$ that for every $j<p-1$ , $f^{(j)} = 0$ , while for every $j\ge p$ , $f^{(j)} = 0 \pmod p$ (zero modulo $p$ ). Additionally, $f^{(p-1)} = v^{(m-1)p} T^p(0) = v^{(m-1)p}u^p$ .

Thus: 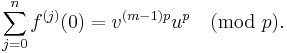$\sum_{j=0}^n f^{(j)}(0) = v^{(m-1)p} u^p \pmod p.$

On the other hand, it follows from the definition of $f$ and of $Î²$ ₁... $Î²$ _$n$ that

$f(x) = \bigg(v^m (x-\beta_1)(x-\beta_2)\cdots(x-\beta_m)\bigg)^p \frac {x^{p-1}}{(p-1)!}.$

Thus for every 1 â¤ $i$ â¤ $n$ , and for every $j$ < $p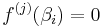$ , $f^{(j)}(\beta_i) = 0$ , while for every 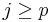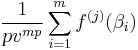$j \ge p$ , ${\frac{1}{pv^{mp}}}\sum_{i=1}^m f^{(j)}(\beta_i)$ is a symmetric polynomial with integer coefficients of degree smaller than $mp$ in $Î²$ ₁... $Î²$ _$n$. According to the fundamental theorem of symmetric polynomials, it is a polynomial with integer coefficients, of degree $mp$ at most, in the elementary symmetric polynomials of $Î²$ ₁... $Î²$ _$n$. The latter are equal (up to a sign) to the coefficients of 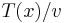$T(x)/v$ , which are integers divided by $v$ .

Therefore for every $j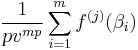$ , ${\frac{1}{pv^{mp}}}\sum_{i=1}^m f^{(j)}(\beta_i)$ is a polynomial with integer coefficients, of degree $mp$ at most, in integers divided by $v$ ; thus it is an integer divided by $v$ ^$mp$. This means that 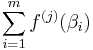$\sum_{i=1}^m f^{(j)}(\beta_i)$ is an integer and is 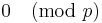$0 \pmod p$ , and so also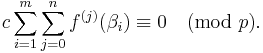 $c\sum_{i=1}^m \sum_{j=0}^n f^{(j)}(\beta_i) \equiv 0 \pmod p.$

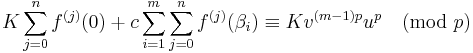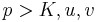To conclude, $K \sum_{j=0}^n f^{(j)}(0) %2B c\sum_{i=1}^m \sum_{j=0}^n f^{(j)}(\beta_i) \equiv K v^{(m-1)p} u^p \pmod p$ . For $p>K,u,v$ , this is non-zero. It is therefore a non-zero integer. So it follows from the vanishing of 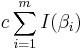$c\sum_{i=1}^m I(\beta_i)$ at the limit where p grows to infinity, that 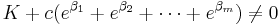$K%2Bc(e^{\beta_1} %2B e^{\beta_2} %2B\cdots%2B e^{\beta_m}) \ne 0$ , and the Lemma is proven.

Lemma B

If $K$ and $c$ (1), $c$ (2), ..., $c$ ( $n$ ) are non-zero integers, and for every $k$ between 1 and $n$ , { $Î²$ ( $k$ )_$i$} ( $i$ = 1, ..., $m$ ( $k$ )) are the roots of a polynomial with integer coefficients $T$ _$k$( $x$ ) = $v$ ( $k$ ) $x$ ^{$m$ ( $k$ )} + ... + $u$ ( $k$ ) with $v$ ( $k$ ), $u$ ( $k$ ) â 0, then

$\begin{align} & K%2Bc(1)(e^{\beta(1)_1} %2B e^{\beta(1)_2} %2B\cdots%2B e^{\beta(1)_{m(1)}}) %2B c(2)(e^{\beta(2)_1} %2B e^{\beta(2)_2} %2B \cdots \\ & \cdots %2B e^{\beta(2)_{m(2)}})%2B \cdots %2B c(n)(e^{\beta(n)_1} %2B e^{\beta(n)_2} %2B\cdots%2B e^{\beta(n)_{m(n)}}) \ne 0. \end{align}$

Proof of Lemma B:

First we note, that the roots of each polynomial $T$ _$k$( $x$ ) remain unchanged following a multiplication of $T$ _$k$( $x$ ) by a non-zero factor. Thus we may choose the polynomials in such a way, that the value of $u$ ( $k$ ) $v$ ( $k$ )^{$m$ ( $k$ ) â 1} is independent of $k$ (otherwise we multiply each polynomial $T$ _$k$( $x$ ) by an appropriate integer factor, say 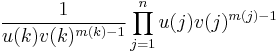${\frac{1}{u(k)v(k)^{m(k)-1}}}\prod_{j=1}^n u(j)v(j)^{m(j)-1}$ ). Thus we assume $u$ ( $k$ ) $v$ ( $k$ )^{$m$ ( $k$ ) â 1} = $U$ for every 1 â¤ $k$ â¤ $n$ , with some integer $U$ .

Following the proof of Lemma A, and defining similarly a function $f$ _$k$( $x$ ) and an integral $I$ _$k$( $s$ ) for every polynomial $T$ _$k$( $x$ ), we get for every 1 â¤ $k$ â¤ $n$ :

$c(k)\sum_{i=1}^{m(k)} I_k(\beta(k)_i) = (K_k%2B c(k)\sum_{i=1}^{m(k)} e^{\beta(k)_i}) \sum_{j=0}^{m(k)p%2Bp-1} f_k^{(j)}(0) - K_k \sum_{j=0}^{m(k)p%2Bp-1} f_k^{(j)}(0) - c(k)\sum_{i=1}^{m(k)} \sum_{j=0}^{m(k)p%2Bp-1} f_k^{(j)}(\beta(k)_i)$

$\equiv \bigg((K_k%2B c(k)\sum_{i=1}^{m(k)} e^{\beta(k)_i})U^p -K_k U^p\bigg) \pmod p.$

For every choice of integer $K$ _$k$; we choose the $K$ _$k$'s so that their sum is $K$ .

By summing up the above equation for all $k$ between 1 and $n$ , the left side vanishes at the limit where $p$ goes to infinity while the right side is

$\equiv \bigg((K%2B \sum_{k=1}^n c(k) \sum_{i=1}^{m(k)} e^{\beta(k)_i})U^p -K U^p\bigg) \pmod p.$

As in the proof of the Lemma A, we choose a prime $p$ > $K$ , $U$ , and it is then obvious that if $K$ is non-zero then

$K%2B \sum_{k=1}^n c(k) \sum_{i=1}^{m(k)} e^{\beta(k)_i}\ne 0,$

and Lemma B is proven.

Lemma C

If $b$ (0), $b$ (1), $b$ (2), ..., $b$ ( $n$ ) are non-zero integers, and $Î³$ (0), $Î³$ (1), ..., $Î³$ ( $n$ ), are distinct algebraic numbers, then

$b(0)e^{\gamma(0)}%2Bb(1)e^{\gamma(1)}%2B\cdots%2B b(n)e^{\gamma(n)}\ne 0.$

Proof of Lemma C:

Let us assume that 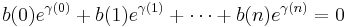$b(0)e^{\gamma(0)}%2Bb(1)e^{\gamma(1)}%2B\cdots%2B b(n)e^{\gamma(n)}= 0$ . We will see that this leads to a contradiction.

First we divide this equation by 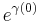$e^{\gamma(0)}$ . Then we get:

$K%2B b(1)e^{\alpha(1)}%2Bb(2)e^{\alpha(2)}%2B\cdots %2B b(n)e^{\alpha(n)} = 0$

with $K$ = $b$ (0) and $Î\pm$ ( $i$ ) = $Î³$ ( $i$ ) â $Î³$ (0) for every 1 â¤ $i$ â¤ $n$ . Since the $Î³$ 's are distinct algebraic numbers, so are the $Î\pm$ 's, and they are also non-zero.

For every $k$ between 1 and $n$ , $Î\pm$ ( $k$ ) is algebraic and so it is a root of a polynomial with integer coefficients: $T$ _$k$( $x$ ) = $v$ ( $k$ ) $x$ ^{$m$ ( $k$ )}+...+ $u$ ( $k$ ) with some non-zero integers $v$ ( $k$ ) and $u$ ( $k$ ) and some positive integer $m$ ( $k$ ). Let us denote its roots $Î\pm$ ( $k$ )₁, $Î\pm$ ( $k$ )₂, ... $Î\pm$ ( $k$ )_{$m$ ( $k$ )} with $Î\pm$ ( $k$ )₁ = $Î\pm$ ( $k$ ).

Let $Ï$ be a function which chooses one element from each of the sequences (1, ..., $m$ (1)), (1, ..., $m$ (2)), ..., (1, ..., $m$ ( $n$ )), such that $Ï$ ( $k$ ) is an integer between 1 and $m$ ( $k$ ). Then according to our assumption:

$\prod_{\{\sigma\}}\left(K %2B b(1)e^{\alpha(1)_{\sigma(1)}}%2Bb(2)e^{\alpha(2)_{\sigma(2)}} %2B \cdots %2B b(n)e^{\alpha(n)_{\sigma(n)}}\right) = 0$

where the product is over all possible choices. The product vanishes because one of the choices is just 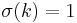$\sigma(k) = 1$ for every $k$ , for which the term vanishes according to our assumption above.

By expanding this product we get a sum of the form:

$\begin{align} & {} K' %2B c(1)\left(e^{\beta(1)_1}%2Be^{\beta(1)_2}%2B\cdots %2Be^{\beta(1)_{\mu(1)}}\right)%2B c(2)\left(e^{\beta(2)_1} %2B e^{\beta(2)_2} %2B\cdots %2B e^{\beta(1)_{\mu(2)}}\right) %2B \cdots \\ & \cdots %2B c(N)\left(e^{\beta(N)_1}%2Be^{\beta(N)_2}%2B\cdots %2Be^{\beta(N)_{\mu(N)}}\right)= 0. \end{align}$

for some non-zero integers $K'$ , $N$ , $c$ (1), ..., $c$ ( $N$ ), $Î¼$ (1), ..., $Î¼$ ( $N$ ), and distinct, non-zero $Î²$ 's.

For every $i$ in 1, ..., $N$ , and every $j$ in 1, ..., $Î¼$ ( $i$ ), $Î²$ ( $i$ )_$j$ is a sum of terms of the form $Î\pm$ ( $k$ )_$r$ ( $k$ in 1, ..., $n$ and $r$ in 1, ..., $m$ ( $k$ )). Because the product was over all possible choices $Ï$ , it follows that for every $i$ and every $k$ , every symmetric polynomial with integer coefficients in $Î²$ ( $i$ )₁... $Î²$ ( $i$ )_{$Î¼$ ( $i$ )} is also symmetric â and thus a symmetric polynomial with integer coefficients â in the set $Î\pm$ ( $k$ )₁, $Î\pm$ ( $k$ )₂, ..., $Î\pm$ ( $k$ )_{$m$ ( $k$ )} (more accurately, the coefficients can also be themselves symmetric polynomials in other $Î\pm$ 's).

Since this set is the set of roots of a polynomial with integer coefficients, the symmetric polynomials are rational numbers (this follows from them being polynomial in the elementary symmetric polynomials of $Î\pm$ ( $k$ )₁, ..., $Î\pm$ ( $k$ )_{$m$ ( $k$ )}, which are integers divided by $v$ ( $k$ ), as explained in the proof of Lemma A).

Therefore $Î²$ ( $i$ )₁, ..., $Î²$ ( $i$ )_{$Î¼$ ( $i$ )} are roots of a polynomial with rational coefficients; this polynomial is 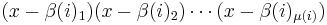$(x-\beta(i)_1)(x-\beta(i)_2)\cdots(x-\beta(i)_{\mu(i)})$ . By multiplying it with an appropriate integer (i.e. the product of all denominators of the coefficients), we get a polynomial with integer coefficients, whose roots are $Î²$ ( $i$ )₁... $Î²$ ( $i$ )_{$Î¼$ ( $i$ )}.

Then, according to Lemma B, this sum cannot be zero, and we have arrived at a contradiction.

Thus Lemma C is proven.

Final step

We turn now to prove the theorem: Let $a$ (1), $a$ (2), ..., $a$ ( $n$ ) be non-zero algebraic numbers, and $Î\pm$ (1), $Î\pm$ (2), ..., $Î\pm$ ( $n$ ) distinct algebraic numbers. Then let us assume that:

$a(1)e^{\alpha(1)}%2Ba(2)e^{\alpha(2)}%2B\cdots %2B a(n)e^{\alpha(n)} = 0. \,$

We will show that this leads to contradiction and thus prove the theorem.

The proof is very similar to that of Lemma C, except that this time the choices are made over the $a$ ( $i$ )'s:

For every $i$ in 1, ..., $n$ , $a$ ( $i$ ) is algebraic, so it is a root of some polynomial with integer coefficients and degree which we denote $d$ ( $i$ ). Let us denote the roots of this polynomial $a$ ( $i$ )₁, $a$ ( $i$ )₂, ..., $a$ ( $i$ )_{$d$ ( $i$ )}, with $a$ ( $i$ )₁ = $a$ ( $i$ ).

Let $Ï$ be a function which chooses one element from each of the sequences (1, ..., $d$ (1)), (1, ..., $d$ (2)), ..., (1, ..., $d$ ( $n$ )), such that for every 1 â¤ $i$ â¤ $n$ , $Ï$ ( $i$ ) is an integer between 1 and $d$ ( $i$ ). Then according to our assumption:

$\prod_{\{\sigma\}}\left(a(1)_{\sigma(1)}e^{\alpha(1)}%2Ba(2)_{\sigma(2)}e^{\alpha(2)} %2B\cdots%2B a(n)_{\sigma(n)} e^{\alpha(n)}\right) = 0$

where the product is over all possible choices. The product vanishes because one of the choices is just $Ï$ ( $i$ ) = 1 for all $i$ , for which the term vanishes according to our assumption above.

By expanding this product we get a sum of the form:

$b(1)e^{\beta(1)}%2B b(2)e^{\beta(2)}%2B \cdots %2B b(N)e^{\beta(N)}= 0.$

for some non-zero integer $N$ , some distinct algebraic $Î²$ (1), $Î²$ (2), ..., $Î²$ ( $N$ ) (these are indeed algebraic because each is a sum of $Î\pm$ 's which are algebraic themselves), and $b$ (1), $b$ (2), ..., $b$ ( $N$ ) are polynomial in $a$ ( $i$ )_$j$ ( $i$ in 1, ..., $n$ and $j$ in 1, ..., $d$ ( $i$ )) with integer coefficients.

Since the product is over all possible choices, each of $b$ (1), $b$ (2), ..., $b$ ( $N$ ) is symmetric in $a$ ( $i$ )₁, ..., $a$ ( $i$ )_{$d$ ( $i$ )} for every $i$ ; therefore each of $b$ (1), $b$ (2), ..., $b$ ( $N$ ) is a polynomial with integer coefficients in elementary symmetric polynomials of the sets { $a$ ( $i$ )₁, ..., $a$ ( $i$ )_{$d$ ( $i$ )}} for every $i$ . Each of the latter is a rational number (as in the proof of Lemma C).

Thus $b$ (1), $b$ (2), ..., $b$ ( $N$ ) are rational numbers, and by multiplying the equation with an appropriate integer factor, we get an identical equation except that now $b$ (1), ..., $b$ ( $N$ ) are all integers.

Therefore, according to Lemma C, the equality cannot hold, and we are led to a contradiction.

This completes the proof.

Note that Lemma A is sufficient to prove that pi is irrational, since otherwise we may write $Ï$ = $k$ / $n$ ( $k$ , $n$ , integers) and then $i$ $Ï$ , â $i$ $Ï$ are the roots of $x$ ² + $k$ ²/ $n$ ²; thus 2 + $e$ ^{$i$ $Ï$} + $e$ ^{â $i$ $Ï$} â 0; but this is false.

Similarly, Lemma C is sufficient to prove that pi is transcendental, since otherwise we would have 1 + $e$ ^{$i$ $Ï$} â 0.

References

^ Sur la fonction exponentielle, Comptes Rendus Acad. Sci. Paris, 77, pages 18â24, 1873.
^ A.O.Gelfond, Transcendental and Algebraic Numbers, translated by Leo F. Boron, Dover Publications, 1960.
^ Ãber die Ludolph'sche Zahl, Sitzungsber. KÃ¶nigl. Preuss. Akad. Wissensch. zu Berlin, 2, pages 679â682, 1882.
^ Zu Hrn. Lindemanns Abhandlung: 'Ãber die Ludolph'sche Zahl' , Sitzungber. KÃ¶nigl. Preuss. Akad. Wissensch. zu Berlin, 2, pages 1067â1086, 1885
^ Daniel Bertrand, Theta functions and transcendence, The Ramanujan Journal 1, pages 339â350, 1997.
^ (French) Proof's Lindemann-Weierstrass (HTML)

LindemannâWeierstrass theorem

Contents