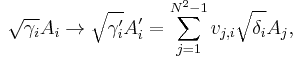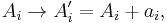Lindblad equation

In quantum mechanics, the Kossakowski–Lindblad equation (after Andrzej Kossakowski and Göran Lindblad) or master equation in the Lindblad form is the most general type of markovian and time-homogeneous master equation describing non-unitary evolution of the density matrix \rho that is trace preserving and completely positive for any initial condition.

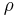The Lindblad master equation for an N-dimensional system's reduced density matrix \ \rho can be written:

\dot\rho=-{i\over\hbar}[H,\rho]%2B\sum_{n,m = 1}^{N^2-1} h_{n,m}\big(-\rho L_m^\dagger L_n-L_m^\dagger L_n\rho%2B2L_n\rho L_m^\dagger\big)

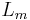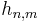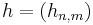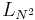where \ H is a (Hermitian) Hamiltonian part, the \ L_m are an arbitrary orthonormal basis of the operators on the system's Hilbert space, and the \ h_{n,m} are constants which determine the dynamics. The coefficient matrix \ h = (h_{n,m}) must be positive to ensure that the equation is trace preserving and completely positive. The summation only runs to \ N^2-1 because we have taken \ L_{N^2} to be proportional to the identity operator, in which case the summand vanishes. Our convention implies that the 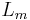\ L_m are traceless for 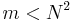\ m<N^2. 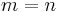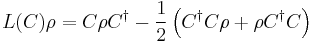The terms in the summation where m=n can be described in terms of the Lindblad superoperator, L(C)\rho=C\rho C^\dagger -\frac{1}{2}\left(C^\dagger C \rho %2B\rho C^\dagger C\right) .

If the 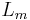\ L_m terms are all zero, then this is the quantum Liouville equation (for a closed system), which is the quantum analog of the classical Liouville equation. A related equation describes the time evolution of the expectation values of observables, it is given by the Ehrenfest theorem.

Note that \ H is not necessarily equal to the self-Hamiltonian of the system. It may also incorporate effective unitary dynamics arising from the system-environment interaction.

Contents

Diagonalization

Since the matrix 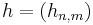\ h = (h_{n,m}) is positive, it can be diagonalized with a unitary transformation u:

u^\dagger h u = \begin{bmatrix} \gamma_1 & 0 & \cdots & 0 \\ 0 & \gamma_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \gamma_{N^2-1} \end{bmatrix}

where the eigenvalues 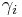\ \gamma_i are non-negative. If we define another orthonormal operator basis

A_i = \sum_{j = 1}^{N^2-1} u_{j,i} L_j

we can rewrite the Lindblad equation in diagonal form

\dot\rho=-{i\over\hbar}[H,\rho]%2B\sum_{i = 1}^{N^2-1} \gamma_{i}\big(A_i\rho A_i^\dagger -\frac{1}{2} \rho A_i^\dagger A_i -\frac{1}{2} A_i^\dagger A_i \rho \big) .

This equation is invariant under a unitary transformation of the Lindblad operators and constants,

\sqrt{\gamma_i} A_i \to \sqrt{\gamma_i'} A_i' = \sum_{j = 1}^{N^2-1} v_{j,i} \sqrt{\delta_i} A_j ,

and also under the inhomogenous transformation

A_i \to A_i' = A_i %2B a_i ,
H \to H' = H %2B \frac{1}{2i} \sum_{j=1}^{N^2-1} \gamma_j (a_j^* A_j - a_j A_J^\dagger) .

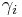However, the first transformation destroys the orthonormality of the operators \ A_i (unless all the \ \gamma_i are equal) and the second transformation destroys the tracelessness. Therefore, up to degeneracies among the 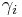\ \gamma_i, the \ A_i of the diagonal form of the Lindblad equation are uniquely determined by the dynamics so long as we require them to be orthonormal and traceless.

Harmonic oscillator example

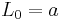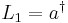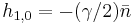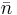The most common Lindblad equation is that describing the damping of a quantum harmonic oscillator, it has \ L_0=a, \ L_1=a^{\dagger}, \ h_{0,1}=-(\gamma/2)(\bar n%2B1), \ h_{1,0}=-(\gamma/2)\bar n with all others \ h_{n,m}=0. Here \bar n is the mean number of excitations in the reservoir damping the oscillator and 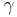\ \gamma is the decay rate. Additional Lindblad operators can be included to model various forms of dephasing and vibrational relaxation. These methods have been incorporated into grid-based density matrix propagation methods.

See also

Open quantum system

References

External links