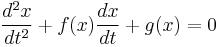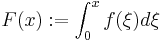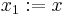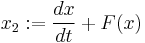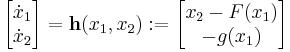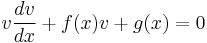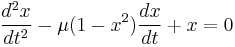Liénard equation

In mathematics, more specifically in the study of dynamical systems and differential equations, a Liénard equation^[1] is a second order differential equation, named after the French physicist Alfred-Marie Liénard.

During the development of radio and vacuum tube technology, Liénard equations were intensely studied as they can be used to model oscillating circuits. Under certain additional assumptions Liénard's theorem guarantees the uniqueness and existence of a limit cycle for such a system.

1 Definition
2 Liénard system
3 Example
4 Liénard's theorem
5 See also
6 Footnotes
7 External links

Definition

Let f and g be two continuously differentiable functions on R, with g an odd function and f an even function then the second order ordinary differential equation of the form

${d^2x \over dt^2}%2Bf(x){dx \over dt}%2Bg(x)=0$

is called the Liénard equation.

Liénard system

The equation can be transformed into an equivalent two-dimensional system of ordinary differential equations. We define

$F(x)�:= \int_0^x f(\xi) d\xi$

$x_1:= x\,$

$x_2:={dx \over dt} %2B F(x)$

then

$\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \end{bmatrix} = \mathbf{h}(x_1, x_2) := \begin{bmatrix} x_2 - F(x_1) \\ -g(x_1) \end{bmatrix}$

is called a Liénard system.

Alternatively, since Liénard equation itself also belongs to autonomous differential equation, the substitution 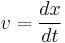$v = {dx \over dt}$ leads the Liénard equation to a first order differential equation:

$v{dv \over dx}%2Bf(x)v%2Bg(x)=0$

which belongs to Abel equation of the second kind.^[2]^[3]

Example

The Van der Pol oscillator

${d^2x \over dt^2}-\mu(1-x^2){dx \over dt} %2Bx= 0$

is a Liénard equation.

Liénard's theorem

A Liénard system has a unique and stable limit cycle surrounding the origin if it satisfies the following additional properties:

g(x) > 0 for all x > 0;
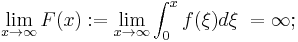
$\lim_{x \to \infty} F(x)�:= \lim_{x \to \infty} \int_0^x f(\xi) d\xi\ = \infty;$
F(x) has exactly one positive root at some value p, where F(x) < 0 for 0 < x < p and F(x) > 0 and monotonic for x > p.

Footnotes

^ Liénard, A. (1928) "Etude des oscillations entretenues," Revue générale de l'électricité 23, pp. 901–912 and 946–954.
^ Liénard equation at eqworld.
^ Abel equation of the second kind at eqworld.

External links

LienardSystem at PlanetMath.