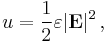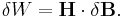Lenz's law

Electromagnetism

Electricity Magnetism
Electrostatics Electric charge Coulomb's law Electric field Electric flux Gauss's law Electric potential energy Electric potential Electrostatic induction Electric dipole moment Polarization density
Magnetostatics Ampère's law Electric current Magnetic field Magnetization Magnetic flux Biot–Savart law Magnetic dipole moment Gauss's law for magnetism
Electrodynamics Lorentz force law emf Electromagnetic induction Faraday’s law Lenz's law Displacement current Maxwell's equations EM field Electromagnetic radiation Liénard–Wiechert potential Maxwell tensor Eddy current
Electrical Network Electrical conduction Electrical resistance Capacitance Inductance Impedance Resonant cavities Waveguides
Covariant formulation Electromagnetic tensor EM Stress-energy tensor Four-current Electromagnetic four-potential
Scientists Ampère Coulomb Faraday Gauss Heaviside Henry Hertz Lorentz Maxwell Tesla Volta Weber Ørsted

Lenz's law /ˈlɛntsɨz lɔː/ is a common way of understanding how electromagnetic circuits obey Newton's third law and the conservation of energy.^[1] Lenz's law is named after Heinrich Lenz, and it says:

An induced electromotive force (emf) always gives rise to a current whose magnetic field opposes the original change in magnetic flux.

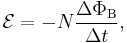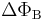Lenz's law is shown with the minus sign in Faraday's law of induction, $\mathcal{E}=-N\frac{\Delta\Phi_\mathrm{B}}{\Delta t},$ which indicates that the induced emf ( $\mathcal{E}$ ) and the change in flux ( $\Delta\Phi_\mathrm{B} \,$ ) have opposite signs.^[2]

For a rigorous mathematical treatment, see electromagnetic induction and Maxwell's equations.

1 Opposing currents
- 1.1 Example
2 Detailed interaction of charges in these currents
- 2.1 Field energy
- 2.2 Conservation of momentum
3 References
4 External links

Opposing currents

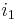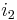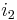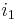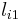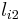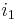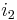If the magnetic field of current $i_1$ induces another current, $i_2$ , the direction of $i_2$ is opposite that of $i_1$ . If these currents are in two circular conductors $l_{i1}$ and $l_{i2}$ respectively, then the currents $i_1$ and $i_2$ must counter-rotate. The opposing currents will repel each other as a result.

Example

Currents bound inside the atoms of strong magnets can create counter-rotating currents in a copper or aluminum pipe. This is done by dropping the magnet through the pipe. When done, the descent of the magnet is observably slower than when dropped outside the pipe.

Detailed interaction of charges in these currents

In electromagnetism, when charges change positions along electric field lines, work is done on them, whether it involves storing potential energy (negative work) or increasing kinetic energy (positive work).

When net positive work is applied to a charge 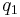$q_1$ , it gains momentum. The net work on 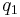$q_1$ thereby generates a magnetic field whose strength (in units of magnetic flux density (1 Tesla = 1 volt-second per square meter)) is proportional to the speed increase of 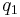$q_1$ . This magnetic field can interact with a neighboring charge 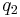$q_2$ , passing on this momentum to it, and in return, 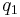$q_1$ loses momentum.

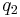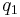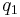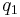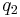$q_2$ can also act on $q_1$ in a similar manner, by which it returns some of the emf that it received from $q_1$ . This back-and-forth component of emf contributes to magnetic inductance. The closer that $q_1$ and $q_2$ are, the greater the effect. When 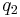$q_2$ is inside a conductive medium such as a thick slab made of copper or aluminum, it more readily reacts to the emf sent to it by 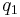$q_1$ . The energy of 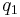$q_1$ is not "instantly" consumed only as heat generated by the current of 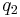$q_2$ but is also stored in two opposing magnetic fields. The energy density of magnetic fields tends to vary by the square of the magnetic field's intensity; however, in the case of magnetically non-linear materials such as ferromagnets and superconductors, this relationship breaks down.

Field energy

The electric field stores energy. The energy density of the electric field is given by:

$u = \frac{1}{2} \varepsilon |\mathbf{E}|^2 \, ,$

In general the incremental amount of work per unit volume δW needed to cause a small change of magnetic field δB is:

$\delta W = \mathbf{H}\cdot\delta\mathbf{B}.$

Conservation of momentum

Momentum must be conserved in the process, so if 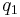$q_1$ is pushed in one direction, then 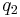$q_2$ ought to be pushed in the other direction by the same force at the same time. However, the situation becomes more complicated when the finite speed of electromagnetic wave propagation is introduced (see retarded potential). This means that for a brief period of time, the total momentum of the two charges are not conserved, implying that the difference should be accounted for by momentum in the fields, as speculated by Richard P. Feynman.^[3] Famous 19th century electrodynamicist James Clerk Maxwell called this the "electromagnetic momentum", although this idea is not generally accepted as a part of standard curricula in physics classes as of 2010.^[4] Yet, such a treatment of fields may be necessary in the case of applying Lenz's law to opposite charges. It is normally assumed that the charges in question are like charges. If they are not, such as a proton and an electron, the interaction is different. An electron generating a magnetic field would generate an emf that causes a proton to change its motion in the same direction as the electron. At first, this might seem to violate the law of conservation of momentum, but of course, such an interaction indeed conserves momentum once taking into account the momentum of electromagnetic fields.

References

^ Schmitt, Ron. Electromagnetics explained. 2002. Retrieved 16 July 2010.
^ Giancoli, Douglas C. (1998). Physics: principles with applications (5th ed.). pp. 624.
^ The Feynman Lectures on Physics: Volume I, Chapter 10, Page 9.
^ Maxwell, James C. A treatise on electricity and magnetism, Volume 2. Retrieved 16 July 2010.

External links

Eddy Currents and Lenz's Law (audio slideshow from the National High Magnetic Field Laboratory)
EduMation A brief video demonstrating Lenz's law
A dramatic demonstration of the effect with an aluminum block in an MRI
Eddy currents produced by magnet and copper pipe.