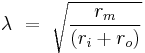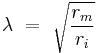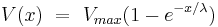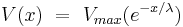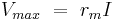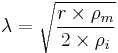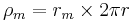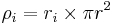Length constant
Length constant is a constant used in neurobiology signified by the Greek letter lambda (λ). The longer a length constant is, the bigger the effect a potential (either an action potential or a current injected at the site) will have along the cell. A long length constant can result in spatial summation, or the algebraic summation of one potential with other potentials from other areas of the cell.
In an action potential (or in a passive spread of signal) in a neuron, the constant λ is
where rm is the resistance across the membrane, ri is the resistance inside the membrane, and ro is the resistance outside the membrane. In calculation, the effects of ro are negligible, so the equation becomes
The resistance across the membrane is a function of the number of open ion channels and the resistance inside the membrane is generally a function of the diameter of the axon. A large diameter is related to a lower ri.
The length constant is used to describe the rise of potential difference across the membrane
The fall of voltage is described by
Where voltage is typically in millivolts, x is distance in millimeters, and λ is in millimeters.
Vmax is defined as the maximum voltage attained in the action potential, where
where rm is the resistance across the membrane and I is the current flow.
Setting for x= λ for the rise of voltage sets V(x) equal to .63 Vmax. This means that the length constant is the distance at which 63% of Vmax has been reached during the rise of voltage.
Setting for x= λ for the fall of voltage sets V(x) equal to .37 Vmax, meaning that the length constant is the distance at which 37% of Vmax has been reached during the fall of voltage.
By resistivity
Expressed with resistivity rather than resistance, the constant λ is (with negligible ro): [1]
Where  is the radius of the neuron.
is the radius of the neuron.
The radius and number 2 come from that:
Expressed in this way, it can be seen that the length constant increases with increasing radius of the neuron.