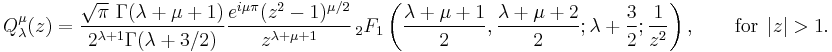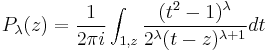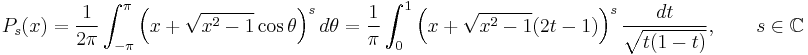Legendre function
In mathematics, the Legendre functions Pλ, Qλ and associated Legendre functions Pμ
λ, Qμ
λ are generalizations of Legendre polynomials to non-integer degree.
Contents |
Differential equation
Associated Legendre functions are solutions of the Legendre equation
where the complex numbers λ and μ are called the degree and order of the associated Legendre functions respectively. Legendre polynomials are the associated Legendre functions of order μ=0.
This is a second order linear equation with three regular singular points (at 1, −1, and ∞). Like all such equations, it can be converted into the hypergeometric differential equation by a change of variable, and its solutions can be expressed using hypergeometric functions.
Definition
These functions may actually be defined for general complex parameters and argument:
where  is the gamma function and
is the gamma function and 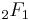 is the hypergeometric function.
is the hypergeometric function.
The second order differential equation has a second solution,  , defined as:
, defined as:
Integral representations
The Legendre functions can be written as contour integrals. For example
where the contour circles around the points 1 and z in the positive direction and does not circle around −1. For real x, we have
Legendre function as characters
The real integral representation of 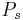 are very useful in the study of harmonic analysis on
are very useful in the study of harmonic analysis on  where
where  is the double coset space of
is the double coset space of  (see Zonal spherical function). Actually the Fourier transform on
(see Zonal spherical function). Actually the Fourier transform on  is given by
is given by
where
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 8", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 332, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_332.htm.
- Courant, Richard; Hilbert, David (1953), Methods of Mathematical Physics, Volume 1, New York: Interscience Publisher, Inc.
- Dunster, T. M. (2010), "Legendre and Related Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/14
- Ivanov, A.B. (2001), "Legendre function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=L/l058030
- Snow, Chester (1952) [1942], Hypergeometric and Legendre functions with applications to integral equations of potential theory, National Bureau of Standards Applied Mathematics Series, No. 19, Washington, D.C.: U. S. Government Printing Office, MR0048145, http://babel.hathitrust.org/cgi/pt?id=mdp.39015023896346
- Whittaker, E. T.; Watson, G. N. (1963), A Course in Modern Analysis, Cambridge University Press, ISBN 978-0-521-58807-2
External links
- Legendre function P on the Wolfram functions site.
- Legendre function Q on the Wolfram functions site.
- Associated Legendre function P on the Wolfram functions site.
- Associated Legendre function Q on the Wolfram functions site.
![(1-x^2)\,y'' -2xy' %2B \left[\lambda(\lambda%2B1) - \frac{\mu^2}{1-x^2}\right]\,y = 0,\,](/2012-wikipedia_en_all_nopic_01_2012/I/fc1a2c177e881d8de8a987eea3194806.png)
![P_{\lambda}^{\mu}(z) = \frac{1}{\Gamma(1-\mu)} \left[\frac{1%2Bz}{1-z}\right]^{\mu/2} \,_2F_1 (-\lambda, \lambda%2B1; 1-\mu; \frac{1-z}{2}),\qquad \text{for } \ |1-z|<2](/2012-wikipedia_en_all_nopic_01_2012/I/6f1ba141b15fded1f9482d7401033da6.png)