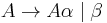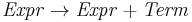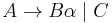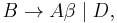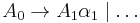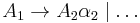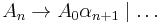Left recursion
In computer science, left recursion is a special case of recursion.
In terms of context-free grammar, a non-terminal r is left-recursive if the left-most symbol in any of r’s ‘alternatives’ either immediately (direct left-recursive) or through some other non-terminal definitions (indirect/hidden left-recursive) rewrites to r again.
Contents |
Definition
"A grammar is left-recursive if we can find some non-terminal A which will eventually derive a sentential form with itself as the left-symbol."[1]
Immediate left recursion
Immediate left recursion occurs in rules of the form
where  and
and  are sequences of nonterminals and terminals, and
are sequences of nonterminals and terminals, and  doesn't start with
doesn't start with  . For example, the rule
. For example, the rule
is immediately left-recursive. The recursive descent parser for this rule might look like:
function Expr()
{
Expr(); match('+'); Term();
}
and a recursive descent parser would fall into infinite recursion when trying to parse a grammar which contains this rule.
Indirect left recursion
Indirect left recursion in its simplest form could be defined as:
possibly giving the derivation 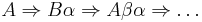
More generally, for the nonterminals 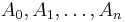 , indirect left recursion can be defined as being of the form:
, indirect left recursion can be defined as being of the form:
where 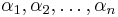 are sequences of nonterminals and terminals.
are sequences of nonterminals and terminals.
Accommodating left recursion in top-down parsing
A formal grammar that contains left recursion cannot be parsed by a LL(k)-parser or other naive recursive descent parser unless it is converted to a weakly equivalent right-recursive form. In contrast, left recursion is preferred for LALR parsers because it results in lower stack usage than right recursion. However, more sophisticated top-down parsers can implement general context-free grammars by use of curtailment. In 2006, Frost and Hafiz describe an algorithm which accommodates ambiguous grammars with direct left-recursive production rules.[2] That algorithm was extended to a complete parsing algorithm to accommodate indirect as well as direct left-recursion in polynomial time, and to generate compact polynomial-size representations of the potentially-exponential number of parse trees for highly-ambiguous grammars by Frost, Hafiz and Callaghan in 2007.[3] The authors then implemented the algorithm as a set of parser combinators written in the Haskell programming language.[4]
Removing left recursion
Removing immediate left recursion
The general algorithm to remove immediate left recursion follows. Several improvements to this method have been made, including the ones described in "Removing Left Recursion from Context-Free Grammars", written by Robert C. Moore.[5] For each rule of the form
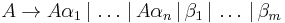
where:
- A is a left-recursive nonterminal
 is a sequence of nonterminals and terminals that is not null (
is a sequence of nonterminals and terminals that is not null (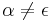 )
) is a sequence of nonterminals and terminals that does not start with A.
is a sequence of nonterminals and terminals that does not start with A.
replace the A-production by the production:
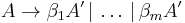
And create a new nonterminal
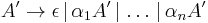
This newly created symbol is often called the "tail", or the "rest".
As an example, consider the rule
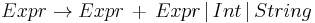
This could be rewritten to avoid left recursion as
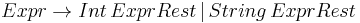
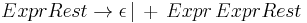
The last rule happens to be equivalent to the slightly shorter form
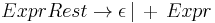
Removing indirect left recursion
If the grammar has no  -productions (no productions of the form
-productions (no productions of the form  ) and is not cyclic (no derivations of the form
) and is not cyclic (no derivations of the form  for any nonterminal A), this general algorithm may be applied to remove indirect left recursion :
for any nonterminal A), this general algorithm may be applied to remove indirect left recursion :
Arrange the nonterminals in some (any) fixed order  .
.
- for i = 1 to n {
- for j = 1 to i – 1 {
-
- let the current
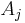 productions be
productions be
- let the current
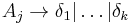
- replace each production
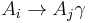 by
by
- replace each production
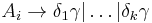
-
- }
- remove direct left recursion for
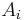
- remove direct left recursion for
- for j = 1 to i – 1 {
- }
Pitfalls
The above transformations remove left-recursion by creating a right-recursive grammar; but this changes the associativity of our rules. Left recursion makes left associativity; right recursion makes right associativity. Example : We start out with a grammar :
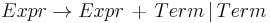

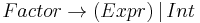
After having applied standard transformations to remove left-recursion, we have the following grammar :
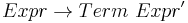
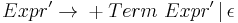
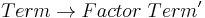
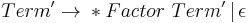
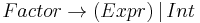
Parsing the string 'a + a + a' with the first grammar in an LALR parser (which can recognize left-recursive grammars) would have resulted in the parse tree:
Expr
/ | \
Expr + Term
/ | \ \
Expr + Term Factor
| | |
Term Factor Int
| |
Factor Int
|
Int
This parse tree grows to the left, indicating that the '+' operator is left associative, representing (a + a) + a.
But now that we've changed the grammar, our parse tree looks like this :
Expr ---
/ \
Term Expr' --
| / | \
Factor + Term Expr' ------
| | | \ \
Int Factor + Term Expr'
| | |
Int Factor  |
Int
|
Int
We can see that the tree grows to the right, representing a + ( a + a). We have changed the associativity of our operator '+', it is now right-associative. While this isn't a problem for the associativity of addition, it would have a significantly different value if this were subtraction.
The problem is that normal arithmetic requires left associativity. Several solutions are: (a) rewrite the grammar to be left recursive, or (b) rewrite the grammar with more nonterminals to force the correct precedence/associativity, or (c) if using YACC or Bison, there are operator declarations, %left, %right and %nonassoc, which tell the parser generator which associativity to force.
See also
References
- ^ Notes on Formal Language Theory and Parsing, James Power, Department of Computer Science National University of Ireland, Maynooth Maynooth, Co. Kildare, Ireland.JPR02
- ^ Frost, R.; R. Hafiz (2006). "A New Top-Down Parsing Algorithm to Accommodate Ambiguity and Left Recursion in Polynomial Time.". ACM SIGPLAN Notices 41 (5): 46–54. doi:10.1145/1149982.1149988. http://portal.acm.org/citation.cfm?id=1149988.
- ^ Frost, R.; R. Hafiz and P. Callaghan (June 2007). "Modular and Efficient Top-Down Parsing for Ambiguous Left-Recursive Grammars.". 10th International Workshop on Parsing Technologies (IWPT), ACL-SIGPARSE (Prague): 109–120. http://acl.ldc.upenn.edu/W/W07/W07-2215.pdf.
- ^ Frost, R.; R. Hafiz and P. Callaghan (January 2008). "Parser Combinators for Ambiguous Left-Recursive Grammars". 10th International Symposium on Practical Aspects of Declarative Languages (PADL), ACM-SIGPLAN. Lecture Notes in Computer Science 4902 (2008): 167–181. doi:10.1007/978-3-540-77442-6_12. ISBN 978-3-540-77441-9. http://cs.uwindsor.ca/~richard/PUBLICATIONS/PADL_08.pdf.
- ^ Moore, Robert C. (May 2000). "Removing Left Recursion from Context-Free Grammars". 6th Applied Natural Language Processing Conference: 249–255. http://acl.ldc.upenn.edu/A/A00/A00-2033.pdf.
External links
- CMU lecture on left-recursion
- Practical Considerations for LALR(1) Grammars
- X-SAIGA - eXecutable SpecificAtIons of GrAmmars