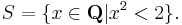Least upper bound axiom
The least upper bound axiom, also abbreviated as the LUB axiom, is an axiom of real analysis stating that the set R of real numbers has the least-upper-bound property. That is, if a nonempty set of real numbers has an upper bound, then it has a least upper bound. It is an axiom in the sense that it cannot be proven by the other real number axioms (namely the order axiom, the field axioms, and the Archimedean axiom). This axiom is very useful since it is essential to the proof that the real number line is a complete metric space.
The rational number line Q does not satisfy the LUB axiom and hence is incomplete. An example is the subset of rational numbers
The number 5 is certainly an upper bound for the set. However, this set has no least upper bound in Q: the LUB in this case is 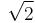 which does not exist in Q, and for any upper bound x ∈ Q, there is another upper bound y ∈ Q with y < x.
which does not exist in Q, and for any upper bound x ∈ Q, there is another upper bound y ∈ Q with y < x.
Equivalent axioms
There are a variety of axioms that are equivalent to the least upper bound axiom. Among these is the following axiom, known as the fundamental axiom of analysis by Körner (2004):
- Every non-decreasing sequence of real numbers which is bounded above tends to a limit.
The fundamental axiom may be shown to be equivalent to the least upper bound axiom, meaning that assuming either one, it is possible to prove that the other holds as a theorem.
The least upper bound axiom is also equivalent to the Bolzano–Weierstrass theorem:
- Every bounded sequence of real numbers has a convergent subsequence.
The axiom is also equivalent to the completeness of the real numbers (in the sense that the real numbers are the only complete Archimedean ordered field). The least upper bound property implies that the limit superior and limit inferior of a bounded sequence are well-defined. When applied to a Cauchy sequence, they coincide and must agree with the limit of the sequence. Conversely, if an Archimedean ordered field were complete, then from any nonempty bounded set S above one can extract an increasing sequence such that no element of S is greater than every element of the sequence. Completeness then implies convergence of the sequence to the least upper bound of S.
See also
References
- Hazewinkel, Michiel, ed. (2001), "Upper and lower bounds", Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=U/u095810
- Körner, Thomas William (2004), A companion to analysis: a second first and first second course in analysis, AMS Chelsea, ISBN 9780821834473