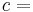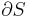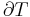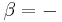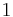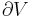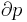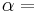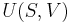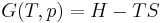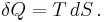Laws of thermodynamics
The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes. The experimentally reproducible distinction between heat and work is at the heart of thermodynamics; thermodynamics has nothing to say about processes in which this distinction cannot be made.
The four principles, or laws, of thermodynamics are:[1][2][3][4][5][6]
- The zeroth law of thermodynamics recognizes that if two systems are in thermal equilibrium with a third, they are also in thermal equilibrium with each other, thus supporting the notions of temperature and heat.
- The first law of thermodynamics distinguishes between two kinds of physical processes, namely energy transfer as work, and energy transfer as heat. It tells how this shows the existence of a mathematical quantity called the internal energy of a system. The internal energy obeys the principle of conservation of energy but work and heat are not defined as separately conserved quantities. Equivalently, the first law of thermodynamics states that perpetual motion machines of the first kind are impossible.
- The second law of thermodynamics distinguishes between reversible and irreversible physical processes. It tells how this shows the existence of a mathematical quantity called the entropy of a system, and thus it expresses the irreversibility of actual physical processes by the statement that the entropy of an isolated macroscopic system never decreases. Equivalently, perpetual motion machines of the second kind are impossible.
- The third law of thermodynamics concerns the entropy of a perfect crystal at absolute zero temperature, and implies that it is impossible to cool a system to exactly absolute zero, or, equivalently, that perpetual motion machines of the third kind are impossible.[7]
Classical thermodynamics describes the exchange of work and heat between systems. It has a special interest in systems that are individually in states of thermodynamic equilibrium. Thermodynamic equilibrium is a condition of systems which are adequately described by only macroscopic variables. Every physical system, however, when microscopically examined, shows apparently random microscopic statistical fluctuations in its thermodynamic variables of state (entropy, temperature, pressure, etc.). These microscopic fluctuations are negligible for systems which are nearly in thermodynamic equilibrium and which are only macroscopically examined. They become important, however, for systems which are nearly in thermodynamic equilibrium when they are microscopically examined, and, exceptionally, for macroscopically examined systems that are in critical states[8], and for macroscopically examined systems that are far from thermodynamic equilibrium.
There have been suggestions of additional laws, but none of them achieve the generality of the four accepted laws, and they are not mentioned in standard textbooks.[1][2][3][4][5][9][10]
The laws of thermodynamics are important fundamental laws in physics and they are applicable in other natural sciences.
Contents |
Zeroth law
The zeroth law of thermodynamics may be stated as follows:
If system A and system B are individually in thermal equilibrium with system C, then system A is in thermal equilibrium with system B
The zeroth law implies that thermal equilibrium, viewed as a binary relation, is a Euclidean relation. If we assume that the binary relationship is also reflexive, then it follows that thermal equilibrium is an equivalence relation. Equivalence relations are also transitive and symmetric. The symmetric relationship allows one to speak of two systems being "in thermal equilibrium with each other", which gives rise to a simpler statement of the zeroth law:
If two systems are in thermal equilibrium with a third, they are in thermal equilibrium with each other
However, this statement requires the implicit assumption of both symmetry and reflexivity, rather than reflexivity alone.
The law is also a statement about measurability. To this effect the law allows the establishment of an empirical parameter, the temperature, as a property of a system such that systems in equilibrium with each other have the same temperature. The notion of transitivity permits a system, for example a gas thermometer, to be used as a device to measure the temperature of another system.
Although the concept of thermodynamic equilibrium is fundamental to thermodynamics, the need to state it explicitly as a law was not widely perceived until Fowler and Planck stated it in the 1930s, long after the first, second, and third law were already widely understood and recognized. Hence it was numbered the zeroth law. The importance of the law as a foundation to the earlier laws is that it allows the definition of temperature in a non-circular way without reference to entropy, its conjugate variable.
First law
The first law of thermodynamics may be expressed by several forms of the fundamental thermodynamic relation for a closed system:
- Increase in internal energy of a system = heat supplied to the system - work done by the system.
- For a thermodynamic cycle, the net heat supplied to the system equals the net work done by the system.
The net change in internal energy is the energy that flows in as heat minus the energy that flows out as the work that the system performs on its environment. Work and heat are not defined as separately conserved quantities; they refer only to processes of exchange of energy.
These statements entail that the internal energy obeys the principle of conservation of energy. The principle of conservation of energy may be stated in several ways:
Energy can be neither created nor destroyed. It can only change forms.
In any process in an isolated system, the total energy remains the same.
Second law
The second law of thermodynamics asserts the existence of a quantity called the entropy of a system and further states that
When two isolated systems in separate but nearby regions of space, each in thermodynamic equilibrium in itself (but not necessarily in equilibrium with each other at first) are at some time allowed to interact, breaking the isolation that separates the two systems, allowing them to exchange matter or energy, they will eventually reach a mutual thermodynamic equilibrium. The sum of the entropies of the initial, isolated systems is less than or equal to the entropy of the final combination of exchanging systems. In the process of reaching a new thermodynamic equilibrium, total entropy has increased, or at least has not decreased.
It follows that the entropy of an isolated macroscopic system never decreases. The second law states that spontaneous natural processes increase entropy overall, or in another formulation that heat can spontaneously be conducted or radiated only from a higher-temperature region to a lower-temperature region, but not the other way around.
The second law refers to a wide variety of processes, reversible and irreversible. Its main import is to tell about irreversibility.
The prime example of irreversibility is in the transfer of heat by conduction or radiation. It was known long before the discovery of the notion of entropy that when two bodies of different temperatures are connected with each other by purely thermal connection, conductive or radiative, then heat always flows from the hotter body to the colder one. This fact is part of the basic idea of heat, and is related also to the so-called zeroth law, though the textbooks' statements of the zeroth law are usually reticent about that, because they have been influenced by Carathéodory's basing his axiomatics on the law of conservation of energy and trying to make heat seem a theoretically derivative concept instead of an axiomatically accepted one. Šilahvý (1997) notes that Carathéodory's approach does not work for the description of irreversible processes that involve both heat conduction and conversion of kinetic energy into internal energy by viscosity (which is another prime example of irreversibility), because "the mechanical power and the rate of heating are not expressible as differential forms in the 'external parameters'".[11]
The second law tells also about kinds of irreversibility other than heat transfer, and the notion of entropy is needed to provide that wider scope of the law.
According to the second law of thermodynamics, in a reversible heat transfer, an element of heat transferred, δQ, is the product of the temperature (T), both of the system and of the source or destination of the heat, with the increment (dS) of the system's conjugate variable, its entropy (S)
The second law defines entropy, which may be viewed not only as a macroscopic variable of classical thermodynamics, but may also be viewed as a measure of deficiency of physical information about the microscopic details of the motion and configuration of the system, given only predictable experimental reproducibility of bulk or macroscopic behavior as specified by macroscopic variables that allow the distinction to be made between heat and work. More exactly, the law asserts that for two given macroscopically specified states of a system, there is a quantity called the difference of entropy between them. The entropy difference tells how much additional microscopic physical information is needed to specify one of the macroscopically specified states, given the macroscopic specification of the other, which is often a conveniently chosen reference state. It is often convenient to presuppose the reference state and not to explicitly state it. A final condition of a natural process always contains microscopically specifiable effects which are not fully and exactly predictable from the macroscopic specification of the initial condition of the process. This is why entropy increases in natural processes. The entropy increase tells how much extra microscopic information is needed to tell the final macroscopically specified state from the initial macroscopically specified state.[12]
Third law
The third law of thermodynamics is usually stated as follows:
This is explained in statistical mechanics by the fact that a perfect crystal has only one possible microstate (microscopic state) at extremely low temperatures: The locations and energies of every atom in a crystal are known and fixed. (In quantum mechanics, the location of each atom is not exactly fixed, but the wavefunction of each atom is fixed in the unique ground state for its position in the crystal.) Entropy is related to the number of possible microstates, and with only one microstate, the entropy is exactly zero.
The third law is also stated in a form that includes non-crystal systems, such as glasses:
As temperature approaches absolute zero, the entropy of a system approaches a minimum.
The minimum, not necessarily zero, is called the residual entropy of the system.
History
In about 1797, Count Rumford (born Benjamin Thompson) showed that mechanical action can generate indefinitely large amounts of heat, so challenging the caloric theory. The historically first established thermodynamic principle which eventually became the second law of thermodynamics was formulated by Sadi Carnot during 1824. By 1860, as formalized in the works of those such as Rudolf Clausius and William Thomson, two established principles of thermodynamics had evolved, the first principle and the second principle, later restated as thermodynamic laws. By 1873, for example, thermodynamicist Josiah Willard Gibbs, in his memoir Graphical Methods in the Thermodynamics of Fluids, clearly stated the first two absolute laws of thermodynamics. Some textbooks throughout the 20th century have numbered the laws differently. In some fields removed from chemistry, the second law was considered to deal with the efficiency of heat engines only, whereas what was called the third law dealt with entropy increases. Directly defining zero points for entropy calculations was not considered to be a law. Gradually, this separation was combined into the second law and the modern third law was widely adopted.
See also
- Conservation law
- Heat death of the universe
- Laws of science
- Table of thermodynamic equations
- Ginsberg's Theorem
References
- ^ a b c Guggenheim, E.A. (1985). Thermodynamics. An Advanced Treatment for Chemists and Physicists, seventh edition, North Holland, Amsterdam, ISBN 0-444-86951-4.
- ^ a b Kittel, C. Kroemer, H. (1980). Thermal Physics, second edition, W.H. Freeman, San Francisco, ISBN 0-7167-1088-9.
- ^ a b Adkins, C.J. (1968). Equilibrium Thermodynamics, McGraw-Hill, London, ISBN 0-07-084057-1.
- ^ a b Kondepudi D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8.
- ^ a b Lebon, G., Jou, D., Casas-Vázquez, J. (2008). Understanding Non-equilibrium Thermodynamics. Foundations, Applications, Frontiers, Springer, Berlin, ISBN 978-3-540-74252-4.
- ^ Chris Vuille; Serway, Raymond A.; Faughn, Jerry S. (2009). College physics. Belmont, CA: Brooks/Cole, Cengage Learning. p. 355. ISBN 0-495-38693-6. http://books.google.ca/books?id=CX0u0mIOZ44C&pg=PT355.
- ^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics, Woodbury NY, ISBN 0-88318-797-3, page 100.
- ^ Balescu, R. (1975). Equilibrium and Nonequilibrium Statistical Mechanics, Wiley, New York, ISBN 0-471-04600-0.
- ^ De Groot, S.R., Mazur, P. (1962). Non-equilibrium Thermodynamics, North Holland, Amsterdam.
- ^ Glansdorff, P., Prigogine, I. (1971). Thermodynamic Theory of Structure, Stability and Fluctuations, Wiley-Interscience, London, ISBN 0-471-30280-5.
- ^ Šilhavý, M. (1997). The Mechanics and Thermodynamics of Continuous Media, Springer, Berlin, ISBN 3-540-58378-5, page 137.
- ^ Ben-Naim, A. (2008). A Farewell to Entropy: Statistical Thermodynamics Based on Information, World Scientific, New Jersey, ISBN 978-981-270-706-2.
Further reading
- Atkins, Peter, 2007. Four Laws That Drive the Universe. OUP Oxford.
- Goldstein, Martin, and Inge F., 1993. The Refrigerator and the Universe. Harvard Univ. Press. A gentle introduction.