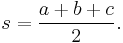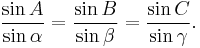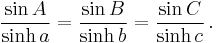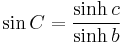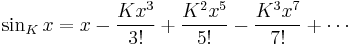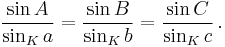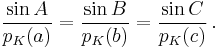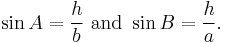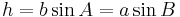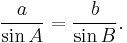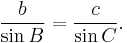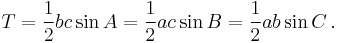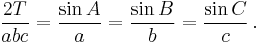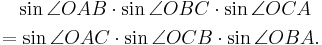Law of sines
In trigonometry, the law of sines (also known as the sine law, sine formula, or sine rule) is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles. According to the law,
where a, b, and c are the lengths of the sides of a triangle, and A, B, and C are the opposite angles (see the figure to the right). Sometimes the law is stated using the reciprocal of this equation:
The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the formula gives two possible values for the enclosed angle, leading to an ambiguous case.
The law of sines is one of two trigonometric equations commonly applied to find lengths and angles in a general triangle, the other being the law of cosines.
Contents |
Examples
The following are examples of how to solve a problem using the law of sines:
Given: side a = 20, side c = 24, and angle C = 40°
Using the law of sines, we conclude that
Or another example of how to solve a problem using the law of sines:
If two sides of the triangle are equal to R and the length of the third side, the chord, is given as 100 feet and the angle C opposite the chord is given in degrees, then the hthe
and
bb
Numeric problems
Like the law of cosines, although the law of sines is mathematically true, it has problems for numeric use. Much precision may be lost if an arcsine is computed when the sine of an angle is close to one.
Some applications
- The sine law can be used to prove the angle sum identity for sine when α and β are each between 0 and 90 degrees.
- To prove this, make an arbitrary triangle with sides a, b, and c with corresponding arbitrary angles A, B and C. Draw a perpendicular to c from angle C. This will split the angle C into two different angles, α and β, that are less than 90 degrees, where we choose to have α to be on the same side as A and β be on the same side as B. Use the sine law identity that relates side c and side a. Solve this equation for the sine of C. Notice that the perpendicular makes two right angles triangles, also note that sin(A) = cos(α), sin(B) = cos(β) and that c = a sin(β) + b sin(α). After making these substitutions you should have sin(C) =sin(α + β) = sin(β)cos(α) + (b/a)sin(α)cos(α). Now apply the sine law identity that relates sides b and a and make the substitutions noted before. Now substitute this expression for (b/a) into the original equation for sin(α + β) and you will have the angle sum identity for α and β in terms of sine.
- The only thing that was used in the proof that was not a definition was the sine law. Thus the sine law is equivalent to the angle sum identity when the angles sum is between 0 and 180 degrees and when each individual angle is between 0 and 90 degrees.
- The sine law along with the prosthaphaeresis and shift identities can be used to prove the law of tangents and Mollweide's formulas (Dresdin 2009, Plane Trigonometry pg. 76–78 ).
The ambiguous case
When using the law of sines to solve triangles, there exists an ambiguous case where two separate triangles can be constructed (i.e., there are two different possible solutions to the triangle).
[[Image:Sine Law - Ambiguous Case.svg]
Given a general triangle ABC, the following conditions would need to be fulfilled for the case to be ambiguous:
- The only information known about the triangle is the angle A and the sides a and b
- The angle A is acute (i.e., A < 90°).
- The side a is shorter than the side b (i.e., a < b).
- The side a is longer than the altitude of a right angled triangle with angle A and hypotenuse b (i.e., a > b sin A).
Given all of the above premises are true, the angle B may be acute or obtuse; meaning, one of the following is true:
or
Relation to the circumcircle
In the identity
the common value of the three fractions is actually the diameter of the triangle's circumcircle.[1] It can be shown that this quantity is equal to
where S is the area of the triangle and s is the semiperimeter
The second equality above is essentially Heron's formula.
Spherical case
In the spherical case, the formula is:
Here, α, β, and γ are the angles at the center of the sphere subtended by the three arcs of the spherical surface triangle a, b, and c, respectively. A, B, and C are the surface angles opposite their respective arcs.
- See also Spherical law of cosines and Half-side formula.
Hyperbolic case
In hyperbolic geometry when the curvature is −1, the law of sines becomes
In the special case when B is a right angle, one gets
which is the analog of the formula in Euclidean geometry expressing the sine of an angle as the opposite side divided by the hypotenuse.
- See also hyperbolic triangle.
Unified formulation
Define a generalized sine function, depending also on a real parameter  :
:
The law of sines in constant curvature  reads as[2]
reads as[2]
By substituing 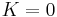 ,
, 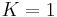 , and
, and 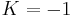 , one obtains respectively the euclidian, spherical, and hyperbolic cases of the law of sines described above.
, one obtains respectively the euclidian, spherical, and hyperbolic cases of the law of sines described above.
Let 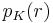 indicate the circumference of a circle of radius
indicate the circumference of a circle of radius  in a space of constant curvature
in a space of constant curvature  . Then
. Then 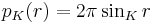 . Therefore the law of sines can also be expressed as:
. Therefore the law of sines can also be expressed as:
This formulation was discovered by Janos Bolyai.[3]
History
The spherical law of sines was discovered in the 10th century. It is variously attributed to al-Khujandi, Abul Wafa Bozjani, Nasir al-Din al-Tusi and Abu Nasr Mansur.[4]
Al-Jayyani's The book of unknown arcs of a sphere in the 11th century introduced the general law of sines.[5] The plane law of sines was later described in the 13th century by Nasīr al-Dīn al-Tūsī. In his On the Sector Figure, he stated the law of sines for plane and spherical triangles, and provided proofs for this law.[6]
Derivation
Make a triangle with the sides a, b, and c, and angles A, B, and C. Draw the altitude from vertex C to the side across c; by definition it divides the original triangle into two right angle triangles. Mark the length of this line h.
It can be observed that:
Therefore
and
Doing the same thing with the line drawn between vertex A and side a will yield:
Alternative derivation
Observe that the area  of the triangle can be written as any of
of the triangle can be written as any of
Multiplying these by 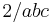 gives
gives
A law of sines for tetrahedra
A corollary of the law of sines as stated above is that in a tetrahedron with vertices O, A, B, C, we have
One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface.
Putting any of the four vertices in the role of O yields four such identities, but in a sense at most three of them are independent: If the "clockwise" sides of three of them are multiplied and the product is inferred to be equal to the product of the "counterclockwise" sides of the same three identities, and then common factors are cancelled from both sides, the result is the fourth identity. One reason to be interested in this "independence" relation is this: It is widely known that three angles are the angles of some triangle if and only if their sum is a half-circle. What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be a half-circle. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The four relations given by this sines law further reduce the number of degrees of freedom, not from 8 down to 4, but only from 8 down to 5, since the fourth constraint is not independent of the first three. Thus the space of all shapes of tetrahedra is 5-dimensional.
See also
- Law of cosines
- Law of tangents
- Mollweide's formula – for checking solutions of triangles
- Half-side formula – for solving spherical triangles
- Surveying
- Gersonides
References
- ^ Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 1-3, 1967
- ^ Russell, Robert A.. "Generalized law of sines". Wolfram Mathworld. http://140.177.205.23/GeneralizedLawofSines.html. Retrieved 25 September 2011.
- ^ Katok, Svetlana (1992). Fuchsian groups. Chicago: University of Chicago Press. p. 22. ISBN 0226425835.
- ^ Sesiano just lists al-Wafa as a contributor. Sesiano, Jacques (2000) "Islamic mathematics" pp. 137— , page 157, in Selin, Helaine; D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 1402002602
- ^ O'Connor, John J.; Robertson, Edmund F., "Abu Abd Allah Muhammad ibn Muadh Al-Jayyani", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Jayyani.html.
- ^ Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. p. 518. ISBN 9780691114859.
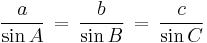
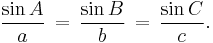
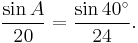
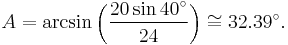
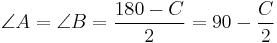
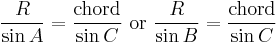
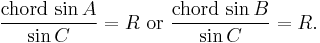
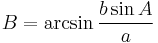
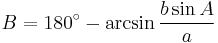
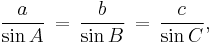
![\begin{align}
\frac{abc} {2S} & {} = \frac{abc} {2\sqrt{s(s-a)(s-b)(s-c)}} \\[6pt]
& {} = \frac {2abc} {\sqrt{(a^2%2Bb^2%2Bc^2)^2-2(a^4%2Bb^4%2Bc^4) }},
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/64530e6bba550d236f78183326b1b4ec.png)