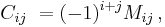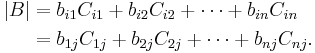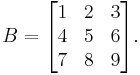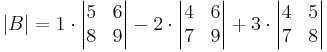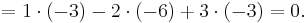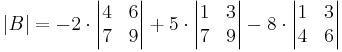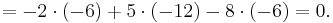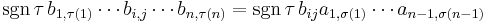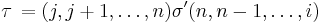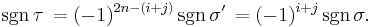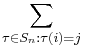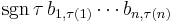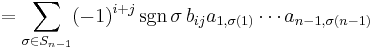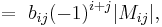Laplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of an n × n square matrix B that is a weighted sum of the determinants of n sub-matrices of B, each of size (n–1) × (n–1). The Laplace expansion is of theoretical interest as one of several ways to view the determinant, as well as of practical use in determinant computation.
The i, j cofactor of B is the scalar Cij defined by
where Mij is the i, j minor matrix of B, that is, the determinant of the (n–1) × (n–1) matrix that results from deleting the i-th row and the j-th column of B.
Then the Laplace expansion is given by the following
Theorem. Suppose B = (bij) is an n × n matrix and i, j ∈ {1, 2, ..., n}.
Then its determinant |B| is given by:
Contents |
Examples
Consider the matrix
The determinant of this matrix can be computed by using the Laplace expansion along the first row:
Alternatively, Laplace expansion along the second column yields
It is easy to see that the result is correct: the matrix is singular because the sum of its first and third column is twice the second column, and hence its determinant is zero.
Proof
Suppose  is an n × n matrix and
is an n × n matrix and 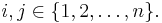 For clarity we also label the entries of
For clarity we also label the entries of  that compose its
that compose its 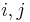 minor matrix
minor matrix 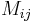 as
as
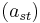 for
for 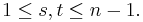
Consider the terms in the expansion of 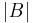 that have
that have 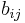 as a factor. Each has the form
as a factor. Each has the form
for some permutation τ ∈ Sn with 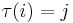 , and a unique and evidently related permutation
, and a unique and evidently related permutation 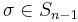 which selects the same minor entries as
which selects the same minor entries as 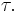 Similarly each choice of
Similarly each choice of  determines a corresponding
determines a corresponding 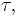 i.e. the correspondence
i.e. the correspondence 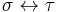 is a bijection between
is a bijection between 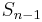 and
and 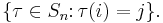 The permutation
The permutation  can be derived from
can be derived from  as follows.
as follows.
Define 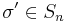 by
by  for
for 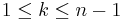 and
and 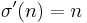 . Then
. Then  and
and
Since the two cycles can be written respectively as 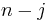 and
and 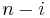 transpositions,
transpositions,
And since the map 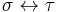 is bijective,
is bijective,
from which the result follows.
References
- David Poole: Linear Algebra. A Modern Introduction. Cengage Learning 2005, ISBN 0534998453, p. 265-267 (restricted online copy at Google Books)
- Harvey E. Rose: Linear Algebra. A Pure Mathematical Approach. Springer 2002, ISBN 3764369051, p. 57-60 (restricted online copy at Google Books)