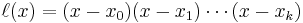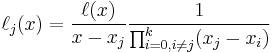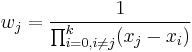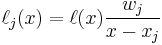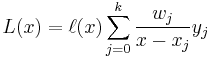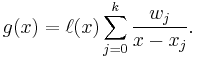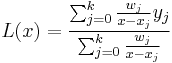Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points 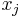 and numbers
and numbers 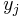 , the Lagrange polynomial is the polynomial of the least degree that at each point
, the Lagrange polynomial is the polynomial of the least degree that at each point 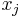 assumes the corresponding value
assumes the corresponding value 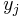 (i.e. the functions coincide at each point). The interpolating polynomial of the least degree is unique, however, and it is therefore more appropriate to speak of "the Lagrange form" of that unique polynomial rather than "the Lagrange interpolation polynomial," since the same polynomial can be arrived at through multiple methods. Although named after Joseph Louis Lagrange, it was first discovered in 1779 by Edward Waring and rediscovered in 1783 by Leonhard Euler.
(i.e. the functions coincide at each point). The interpolating polynomial of the least degree is unique, however, and it is therefore more appropriate to speak of "the Lagrange form" of that unique polynomial rather than "the Lagrange interpolation polynomial," since the same polynomial can be arrived at through multiple methods. Although named after Joseph Louis Lagrange, it was first discovered in 1779 by Edward Waring and rediscovered in 1783 by Leonhard Euler.
Lagrange interpolation is susceptible to Runge's phenomenon, and the fact that changing the interpolation points requires recalculating the entire interpolant can make Newton polynomials easier to use. Lagrange polynomials are used in the Newton-Cotes method of numerical integration and in Shamir's secret sharing scheme in Cryptography.
Contents |
Definition
Given a set of k + 1 data points
where no two 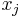 are the same, the interpolation polynomial in the Lagrange form is a linear combination
are the same, the interpolation polynomial in the Lagrange form is a linear combination
of Lagrange basis polynomials
Note how, given the initial assumption that no two  are the same,
are the same, 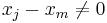 , so this expression is always well-defined. The reason pairs
, so this expression is always well-defined. The reason pairs 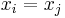 with
with 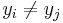 are not allowed is that no interpolation function
are not allowed is that no interpolation function  such that
such that 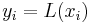 would exist; a function can only get one value for each argument
would exist; a function can only get one value for each argument  . On the other hand, if also
. On the other hand, if also 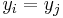 , then those two points would actually be one single point.
, then those two points would actually be one single point.
For all 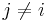 ,
, 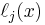 includes the term
includes the term 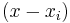 in the numerator, so the whole product will be zero at
in the numerator, so the whole product will be zero at 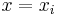 :
:
On the other hand,
In other words, all basis polynomials are zero at 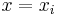 , except
, except 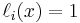 , because it lacks the
, because it lacks the 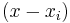 term.
term.
It follows that 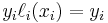 , so at each point
, so at each point  ,
, 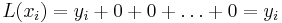 , showing that
, showing that  interpolates the function exactly.
interpolates the function exactly.
Proof
Function L(x) being sought is a polynomial in  of the least degree that interpolates the given data set; that is, assumes value
of the least degree that interpolates the given data set; that is, assumes value 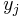 at the corresponding
at the corresponding 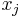 for all data points
for all data points  :
:
Observe that:
- In
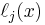 there are k terms in the product and each term contains one x, so L(x) (which is a sum of these k-degree polynomials) must also be a k-degree polynomial.
there are k terms in the product and each term contains one x, so L(x) (which is a sum of these k-degree polynomials) must also be a k-degree polynomial. 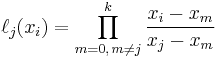
Watch what happens if we expand this product. Because the product skips  , If
, If  then all terms are
then all terms are 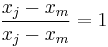 (except where
(except where 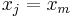 but that case is impossible as pointed out in the definition section---if you tried to write out that term you'd find that
but that case is impossible as pointed out in the definition section---if you tried to write out that term you'd find that 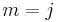 and since
and since 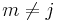 ,
, 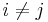 , contrary to
, contrary to 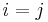 ). Also if
). Also if 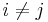 then since
then since 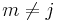 doesn't preclude it, one term in the product will be for
doesn't preclude it, one term in the product will be for 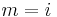 , i.e.
, i.e. 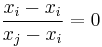 , zeroing the entire product. So
, zeroing the entire product. So
where 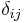 is the Kronecker delta. So:
is the Kronecker delta. So:
Thus the function L(x) is a polynomial with degree at most k and where 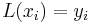 .
.
Additionally, the interpolating polynomial is unique, as shown by the unisolvence theorem at Polynomial interpolation.
Main idea
Solving an interpolation problem leads to a problem in linear algebra where we have to solve a matrix. Using a standard monomial basis for our interpolation polynomial we get the Vandermonde matrix. By choosing another basis, the Lagrange basis, we get the much simpler identity matrix = δi,j which we can solve instantly: the Lagrange basis inverts the Vandermonde matrix.
This construction is the same as the Chinese Remainder Theorem. Instead of checking for remainders of integers modulo prime numbers, we are checking for remainders of polynomials when divided by linears.
Examples
Example 1
Find an interpolation formula for ƒ(x) = tan(x) given this set of known values:
The basis polynomials are:
Thus the interpolating polynomial then is
Example 2
We wish to interpolate ƒ(x) = x2 over the range 1 ≤ x ≤ 3, given these three points:
The interpolating polynomial is:
Example 3
We wish to interpolate ƒ(x) = x3 over the range 1 ≤ x ≤ 3, given these 3 points:
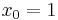 |
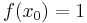 |
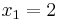 |
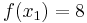 |
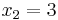 |
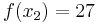 |
The interpolating polynomial is:
Notes
The Lagrange form of the interpolation polynomial shows the linear character of polynomial interpolation and the uniqueness of the interpolation polynomial. Therefore, it is preferred in proofs and theoretical arguments. Uniqueness can also be seen from the invertibility of the Vandermonde matrix, due to the non-vanishing of the Vandermonde determinant.
But, as can be seen from the construction, each time a node xk changes, all Lagrange basis polynomials have to be recalculated. A better form of the interpolation polynomial for practical (or computational) purposes is the barycentric form of the Lagrange interpolation (see below) or Newton polynomials.
Lagrange and other interpolation at equally spaced points, as in the example above, yield a polynomial oscillating above and below the true function. This behaviour tends to grow with the number of points, leading to a divergence known as Runge's phenomenon; the problem may be eliminated by choosing interpolation points at Chebyshev nodes.
The Lagrange basis polynomials can be used in numerical integration to derive the Newton–Cotes formulas.
Barycentric interpolation
Using
we can rewrite the Lagrange basis polynomials as
or, by defining the barycentric weights[1]
we can simply write
which is commonly referred to as the first form of the barycentric interpolation formula.
The advantage of this representation is that the interpolation polynomial may now be evaluated as
which, if the weights 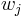 have been pre-computed, requires only
have been pre-computed, requires only 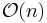 operations (evaluating
operations (evaluating 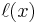 and the weights
and the weights 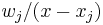 ) as opposed to
) as opposed to 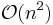 for evaluating the Lagrange basis polynomials
for evaluating the Lagrange basis polynomials 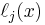 individually.
individually.
The barycentric interpolation formula can also easily be updated to incorporate a new node 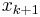 by dividing each of the
by dividing each of the 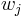 ,
, 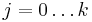 by
by 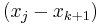 and constructing the new
and constructing the new 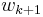 as above.
as above.
We can further simplify the first form by first considering the barycentric interpolation of the constant function 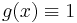 :
:
Dividing 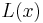 by
by 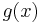 does not modify the interpolation, yet yields
does not modify the interpolation, yet yields
which is referred to as the second form or true form of the barycentric interpolation formula. This second form has the advantage that 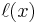 need not be evaluated for each evaluation of
need not be evaluated for each evaluation of 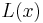 .
.
Finite fields
The Lagrange polynomial can also be computed in finite fields. This has applications in cryptography, such as in Shamir's Secret Sharing scheme.
See also
- Polynomial interpolation
- Neville's algorithm
- Newton form of the interpolation polynomial
- Bernstein form of the interpolation polynomial
- Newton–Cotes formulas
- Lebesgue constant (interpolation)
- The Chebfun system
References
- ^ Jean-Paul Berrut, Lloyd N. Trefethen (2004). "Barycentric Lagrange Interpolation". SIAM Review 46 (3): 501–517. doi:10.1137/S0036144502417715.
External links
- ALGLIB has an implementations in C++ / C# / VBA / Pascal.
- GSL has a polynomial interpolation code in C
- Lagrange Method of Interpolation — Notes, PPT, Mathcad, Mathematica, MATLAB, Maple at Holistic Numerical Methods Institute
- Lagrange interpolation polynomial on www.math-linux.com
- Weisstein, Eric W., "Lagrange Interpolating Polynomial" from MathWorld.
- Estimate of the error in Lagrange Polynomial Approximation at ProofWiki
- Module for Lagrange Polynomials by John H. Mathews
- Dynamic Lagrange interpolation with JSXGraph
- Numerical computing with functions: The Chebfun Project
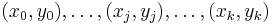
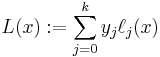
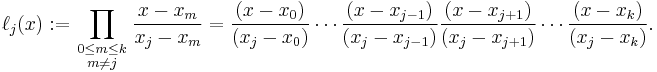
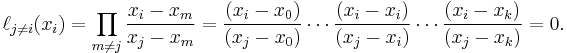
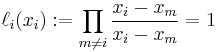

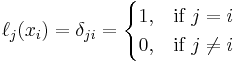
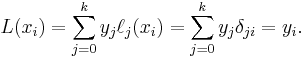
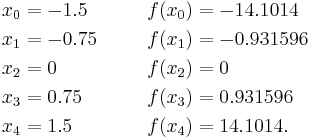
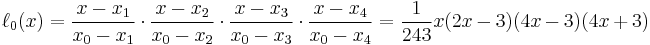
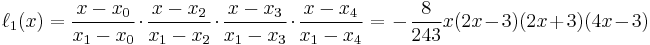
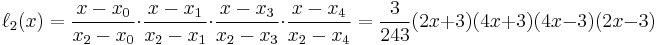
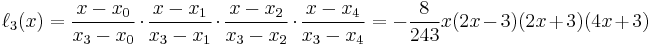
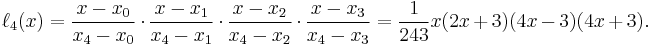
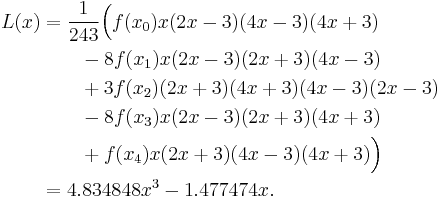
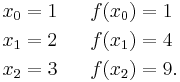
![\begin{align}
L(x) &= {1}\cdot{x - 2 \over 1 - 2}\cdot{x - 3 \over 1 - 3}%2B{4}\cdot{x - 1 \over 2 - 1}\cdot{x - 3 \over 2 - 3}%2B{9}\cdot{x - 1 \over 3 - 1}\cdot{x - 2 \over 3 - 2} \\[10pt]
&= x^2.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/1a33bf2ae75a713617a39b2582aedecb.png)
![\begin{align}
L(x) &= {1}\cdot{x - 2 \over 1 - 2}\cdot{x - 3 \over 1 - 3}%2B{8}\cdot{x - 1 \over 2 - 1}\cdot{x - 3 \over 2 - 3}%2B{27}\cdot{x - 1 \over 3 - 1}\cdot{x - 2 \over 3 - 2} \\[8pt]
&= 6x^2 - 11x %2B 6.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/a7129e7f149df9317e90f677f92757d7.png)