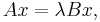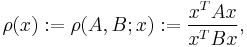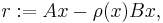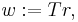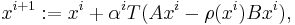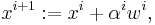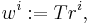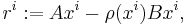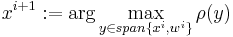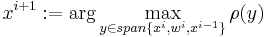LOBPCG

Locally Optimal Block Preconditioned Conjugate Gradient Method (LOBPCG) is an algorithm, proposed in (Knyazev, 2001), for finding the largest (or smallest) eigenvalues and the corresponding eigenvectors of a symmetric positive definite generalized eigenvalue problem.

A x= \lambda B x,

for a given pair 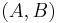(A, B) of complex Hermitian or real symmetric matrices, where the matrix B is also assumed positive-definite.

The method performs an iterative maximization (or minimization) of the generalized Rayleigh quotient

\rho(x)�:= \rho(A,B; x)�:=\frac{x^T A x}{x^T B x},

which results in finding largest (or smallest) eigenpairs of 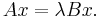A x= \lambda B x.

The direction of the steepest accent, which is the gradient, of the generalized Rayleigh quotient is positively proportional to the vector

r�:= Ax - \rho(x) Bx,

called the eigenvector residual. If a preconditioner T is available, it is applied to the residual giving vector

w�:= Tr,

called the preconditioned residual. Without preconditioning, we set 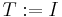T�:= I and so 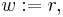w�:= r,. An iterative method

x^{i%2B1}�:= x^i %2B \alpha^i T(Ax^i - \rho(x^i) Bx^i),

or, in short,

x^{i%2B1}�:= x^i %2B \alpha^i w^i,\,
w^i�:= Tr^i,\,
r^i�:= Ax^i - \rho(x^i) Bx^i,

is known as preconditioned steepest accent (or descent), where the scalar 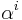\alpha^i is called the step size. The optimal step size can be determined by maximizing the Rayleigh quotient, i.e.,

x^{i%2B1}�:= \arg\max_{y\in span\{x^i,w^i\}} \rho(y)

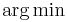(or \arg\min in case of minimizing), in which case the method is called locally optimal. To further accelerate the convergence of the locally optimal precondiitoned steepest accent (or descent), one can add one extra vector to the two-term recurrence relation to make it three-term:

x^{i%2B1}�:= \arg\max_{y\in span\{x^i,w^i,x^{i-1}\}} \rho(y)

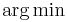(use \arg\min in case of minimizing). The maximization/minimization of the Rayleigh quotient in a 3-dimensional subspace can be performed numerically by the Rayleigh-Ritz method.

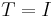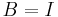This is a single-vector version of the LOBPCG method. It is one of possible generalization of the preconditioned conjugate gradient linear solvers to the case of symmetric eigenvalue problems. Even in the trivial case T=I and B=I the resulting approximation with 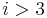i>3 will be different from that obtained by the Lanczos algorithm, although both approximations will belong to the same Krylov subspace.

Iterating several approximate eigenvectors together in a block in a similar locally optimal fashion, gives the full block version of the LOBPCG. It allows robust computation of eigenvectors corresponding to nearly-multiple eigenvalues.

An implementation of LOBPCG is available in the public software package BLOPEX, maintained by Andrew Knyazev. The LOBPCG algorithm is also implemented in many other libraries, e.g.,: ABINIT, Octopus (software), PESCAN, Anasazi (Trilinos), SciPy, NGSolve, and PYFEMax.

References

Knyazev, A.V. (2001), "Toward the Optimal Preconditioned Eigensolver: Locally Optimal Block Preconditioned Conjugate Gradient Method", SIAM Journal on Scientific Computing 23 (2): 517–541, doi:10.1137/S1064827500366124 

Key concepts
Problems
Hardware
Software