L-reduction

In computer science, in particular in the study of approximation algorithms, an L-reduction ("linear reduction") is a transformation of optimization problems which linearly preserves approximability features. L-reductions in studies of approximability of optimization problems play a similar role to that of polynomial reductions in the studies of computational complexity of decision problems.

The term L reduction is sometimes used to refer to log-space reductions, by analogy with the complexity class L, but this is a different concept.

1 Definition
2 Properties
3 See also
4 References

Definition

Let A and B be optimization problems and c_A and c_B their respective cost functions. A pair of functions f and g is an L-reduction if all of the following conditions are met:

functions f and g are computable in polynomial time,
if x is an instance of problem A, then f(x) is an instance of problem B,
if y is a solution to f(x), then g(y) is a solution to x,
there exists a positive constant α such that

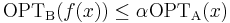$\mathrm{OPT_B}(f(x)) \le \alpha \mathrm{OPT_A}(x)$ ,

there exists a positive constant β such that for every solution y to f(x)

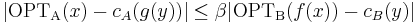$|\mathrm{OPT_A}(x)-c_A(g(y))| \le \beta |\mathrm{OPT_B}(f(x))-c_B(y)|$ .

Properties

Let a (1±ε)-approximation algorithm f for a problem A be such that 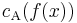$c_\mathrm{A}(f(x))$ is at most 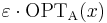$\varepsilon \cdot \mathrm{OPT_A}(x)$ away from 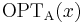$\mathrm{OPT_A}(x)$ , for every instance x. (In this notation, + implicitly means a minimization problem, and 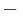$-$ means a maximization problem.)

The main point of an L-reduction is the following: given a (f,g,α,β) L-reduction from problem A to problem B, and a (1±ε)-approximation algorithm for B, we obtain a polynomial-time (1±δ)-approximation algorithm for A where 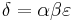$\delta = \alpha \beta \varepsilon$ .^[1]^[2] This implies that if B has a polynomial-time approximation scheme then so does A.

References

^ Kann, Viggo (1992). On the Approximability of NP-complete Optimization Problems. Royal Institute of Technology, Sweden. ISBN 91-7170-082-X.
^ Christos H. Papadimitriou; Mihalis Yannakakis (1988). "Optimization, Approximation, and Complexity Classes". STOC '88: Proceedings of the twentieth annual ACM Symposium on Theory of Computing. doi:10.1145/62212.62233.

Pierluigi Crescenzi: A Short Guide to Approximation Preserving Reductions. In: Proceedings of the Twelfth Annual IEEE Conference on Computational Complexity, June 24-27, 1997, Ulm, Germany. Pages 262-273. IEEE Computer Society Press, 1997. ISBN 0-8186-7907-7
G. Ausiello, P. Crescenzi, G. Gambosi, V. Kann, A. Marchetti-Spaccamela, M. Protasi. Complexity and Approximation. Combinatorial optimization problems and their approximability properties. 1999, Springer. ISBN 3-540-65431-3

L-reduction

Contents

Definition

Properties

See also

References