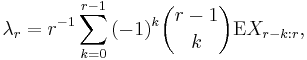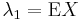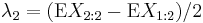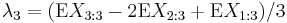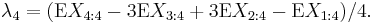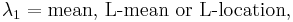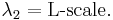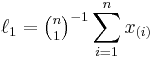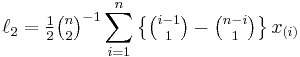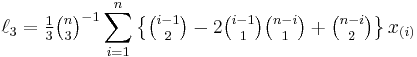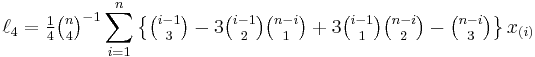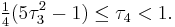L-moment

In statistics, L-moments[1][2][3] are statistics used to summarize the shape of a probability distribution. They are analogous to conventional moments in that they can be used to calculate quantities analogous to standard deviation, skewness and kurtosis, termed the L-scale, L-skewness and L-kurtosis respectively (the L-mean is identical to the conventional mean). Standardised L-moments are called L-moment ratios and these are analogous to standardized moments.

L-moments differ from conventional moments in that they are calculated using linear combinations of the ordered data; the "l" in "linear" is what leads to the name being "L-moments". Just as for conventional moments, a theoretical distribution has a set of population L-moments. Estimates of the population L-moments (sample L-moments) can be defined for a sample from the population.

Contents

Population L-moments

For a random variable X, the rth population L-moment is[1]

\lambda_r = r^{-1} \sum_{k=0}^{r-1} {(-1)^k \binom{r-1}{k} \mathrm{E}X_{r-k:r}},

where Xk:n denotes the kth order statistic (kth smallest value) in an independent sample of size n from the distribution of X and 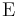\mathrm{E} denotes expected value. In particular, the first four population L-moments are

\lambda_1 = \mathrm{E}X
\lambda_2 = (\mathrm{E}X_{2:2} - \mathrm{E}X_{1:2})/2
\lambda_3 = (\mathrm{E}X_{3:3} - 2\mathrm{E}X_{2:3} %2B \mathrm{E}X_{1:3})/3
\lambda_4 = (\mathrm{E}X_{4:4} - 3\mathrm{E}X_{3:4} %2B 3\mathrm{E}X_{2:4} - \mathrm{E}X_{1:4})/4.

The first two of these L-moments have conventional names:

\lambda_1 = \text{mean, L-mean or L-location},
\lambda_2 = \text{L-scale}.

The L-scale is equal to half the mean difference.[4]

Sample L-moments

Direct estimators for the first four L-moments in a finite sample of n observations are[5]:

\ell_1 = {\tbinom{n}{1}}^{-1} \sum_{i=1}^n x_{(i)}
\ell_2 = \tfrac{1}{2} {\tbinom{n}{2}}^{-1} \sum_{i=1}^n \left\{ \tbinom{i-1}{1} - \tbinom{n-i}{1} \right\} x_{(i)}
\ell_3 = \tfrac{1}{3} {\tbinom{n}{3}}^{-1} \sum_{i=1}^n \left\{ \tbinom{i-1}{2} - 2\tbinom{i-1}{1}\tbinom{n-i}{1} %2B \tbinom{n-i}{2} \right\} x_{(i)}
\ell_4 = \tfrac{1}{4} {\tbinom{n}{4}}^{-1} \sum_{i=1}^n \left\{ \tbinom{i-1}{3} - 3\tbinom{i-1}{2}\tbinom{n-i}{1} %2B 3\tbinom{i-1}{1}\tbinom{n-i}{2} - \tbinom{n-i}{3} \right\} x_{(i)}

where x(i) is the ith order statistic and 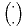\tbinom{\cdot}{\cdot} is a binomial coefficient. Sample L-moments can also be defined indirectly in terms of probability weighted moments,[1] which leads to a more efficient algorithm for their computation.[5]

L-moment ratios

A set of L-moment ratios, or scaled L-moments, is defined by

\tau_r = \lambda_r / \lambda_2, \qquad r=3,4, \dots.

The most useful of these are 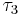\tau_3, called the L-skewness, and 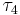\tau_4, the L-kurtosis.

L-moment ratios lie within the interval (–1, 1). Tighter bounds can be found for some specific L-moment ratios; in particular, the L-kurtosis 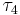\tau_4 lies in [-¼,1), and

\tfrac{1}{4}(5\tau_3^2-1) \leq \tau_4 < 1.[1]

A quantity analogous to the coefficient of variation, but based on L-moments, can also be defined: 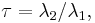\tau = \lambda_2 / \lambda_1, which is called the "coefficient of L-variation", or "L-CV". For a non-negative random variable, this lies in the interval (0,1)[1] and is identical to the Gini coefficient.

Usage

There are two common ways that L-moments are used:

  1. As summary statistics for data.
  2. To derive estimates for the parameters of probability distributions.

In statistics the latter is most commonly done using maximum likelihood methods or using the method of moments, however using L-moments provides an alternative method of parameter estimation. The former can also be performed using conventional moments, however using L-moments provides many advantages. As an example consider a dataset with a few data points and one outlying data value. If the ordinary standard deviation of this data set is taken it will be highly influenced by this one point: however, if the L-scale is taken it will be far less sensitive to this data value. Consequently L-moments are far more meaningful when dealing with outliers in data than conventional moments. One example of this is using L-moments as summary statistics in extreme value theory (EVT).

Another advantage L-moments have over conventional moments is that their existence only requires the random variable to have finite mean, so the L-moments exist even if the higher conventional moments do not exist (for example, for Student's t distribution with low degrees of freedom). A finite variance is required in addition in order for the standard errors of estimates of the L-moments to be finite.[1]

Some appearances of L-moments in the statistical literature include the book by David & Nagaraja (2003, Section 9.9)[6] and a number of papers.[7][8][9][10][11] A number of favourable comparisons of L-moments with ordinary moments have been reported.[12][13]

Values for some common distributions

The table below gives expressions for the first two L-moments and numerical values of the first two L-moment ratios of some common continuous probability distributions with constant L-moment ratios.[1][4] More complex expressions have been derived for some further distributions for which the L-moment ratios vary with one or more of the distributional parameters, including the log-normal, Gamma, generalized Pareto, generalized extreme value, and generalized logistic distributions.[1]

Distribution Parameters mean, λ1 L-scale, λ2 L-skewness, τ3 L-kurtosis, τ4
Uniform a, b (a+b) / 2 (b–a) / 6 0 0
Logistic μ, s μ s 0 ⅙ = 0.1667
Normal μ, σ2 μ σ / √π 0 0.1226
Laplace μ, b μ 3b / 4 0 1 / (3√2) = 0.2357
Student's t, 2 d.f. ν = 2 0 π/23/2 = 1.111 0 ⅜ = 0.375
Student's t, 4 d.f. ν = 4 0 15π/64 = 0.7363 0 111/512 = 0.2168
Exponential λ 1 / λ 1 / (2λ) ⅓ = 0.3333 ⅙ = 0.1667
Gumbel μ, β μ + γβ β log 2 0.1699 0.1504

The notation for the parameters of each distribution is the same as that used in the linked article. In the expression for the mean of the Gumbel distribution, γ is the Euler–Mascheroni constant 0.57721… .

Extensions

Trimmed L-moments are generalizations of L-moments that give zero weight to extreme observations. They are therefore more robust to the presence of outliers, and unlike L-moments they may be well-defined for distributions for which the mean does not exist, such as the Cauchy distribution.[14]

See also

References

  1. ^ a b c d e f g h Hosking, J.R.M. (1990). "L-moments: analysis and estimation of distributions using linear combinations of order statistics". Journal of the Royal Statistical Society, Series B 52: 105–124. JSTOR 2345653. 
  2. ^ Hosking, J.R.M. (1992). "Moments or L moments? An example comparing two measures of distributional shape". The American Statistician 46 (3): 186–189. JSTOR 2685210. 
  3. ^ Hosking, J.R.M. (2006). "On the characterization of distributions by their L-moments". Journal of Statistical Planning and Inference 136: 193–198. 
  4. ^ a b Jones, M.C. (2002). "Student's Simplest Distribution". Journal of the Royal Statistical Society. Series D (The Statistician) 51 (1): 41–49. JSTOR 3650389. 
  5. ^ a b Wang, Q. J. (1996). "Direct Sample Estimators of L Moments". Water Resources Research 32 (12): 3617–3619. doi:10.1029/96WR02675. 
  6. ^ David, H.A. & Nagaraja, H.N. (2003) Order Statistics, 3rd Edition. Wiley. ISBN 0-471-38926-9
  7. ^ Serfling, R. & Xiao, P. (2007) A contribution to multivariate L-moments: L-comoment matrices. Journal of Multivariate Analysis, 98, 1765–1781.
  8. ^ Delicado, P. & N. Goriab M.N. (2008) A small sample comparison of maximum likelihood, moments and L-moments methods for the asymmetric exponential power distribution. Computational Statistics & Data Analysis, 52, 1661–1673
  9. ^ Alkasasbeh, M.R., Raqab, M.Z. (2009) Estimation of the generalized logistic distribution parameters: comparative study. Statistical Methodology, 6(3), 262–279.
  10. ^ Jones, M.C. (2004) On some expressions for variance, covariance, skewness and L-moments. Journal of Statistical Planning and Inference, 126, 97–106. doi:10.1016/j.jspi.2003.09.001
  11. ^ Jones, M.C. (2009) Kumaraswamy's distribution: A beta-type distribution with some tractability advantages. Statistical Methodology, 6 (1), 70–81.
  12. ^ Royston, P. (1992). Which measures of skewness and kurtosis are best? Statistics in Medicine, 11, 333–343. doi:10.1002/sim.4780110306
  13. ^ Ulrych, T. J., Velis, D. R., Woodbury, A. D., Sacchi, M. D. (2000) L-moments and C-moments. Stochastic Environmental Research and Risk Assessment, 14 (1), 50–68.
  14. ^ Elamir, Elsayed A. H.; Seheult, Allan H. (2003). "Trimmed L-moments". Computational Statistics & Data Analysis 43 (3): 299–314. doi:10.1016/S0167-9473(02)00250-5. 

External links
 
Continuous data
Location
Dispersion
Shape
Count data
Summary tables
Dependence
Statistical graphics