L-estimator
In robust statistics, an L-estimator is an estimator which equals a linear combination of order statistics of the measurements.
Consider, for example, the median. Given n measurements  , where n is odd, the median equals
, where n is odd, the median equals 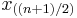 , the
, the 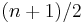 th order statistic (for
th order statistic (for 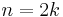 even, it is the average of two order statistics:
even, it is the average of two order statistics: 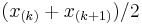 ). The median is therefore a simple example of an L-estimator. Other examples include the trimean, the trimmed mean, and the Winsorized mean.
). The median is therefore a simple example of an L-estimator. Other examples include the trimean, the trimmed mean, and the Winsorized mean.
Not all L-estimators are robust: the minimum, maximum, mean, and mid-range are all L-estimators, but have a breakdown point of 0. The breakdown point is defined as the fraction of the measurements which can be arbitrarily changed without causing the resulting estimate to tend to infinity (i.e., to "break down"). The breakdown point of an L-estimator is given by the closest order statistic to the minimum or maximum: for instance, the median has a breakdown point of 50% (the highest possible), and a n% trimmed or Winsorized mean has a breakdown point of n%.
See also
References
- Huber, Peter J. (2004). Robust statistics. New York: Wiley-Interscience. ISBN 0-471-65072-2.
- Shao, Jun (2003). Mathematical statistics. Berlin: Springer-Verlag. pp. sec. 5.2.2. ISBN 0-387-95382-5.
- Fraiman, Ricardo; Meloche, Jean; Garcia-Escudero, Luis; Gordaliza, Alfonso; He, Xuming; Maronna, Ricardo; Yohai, Victor; Sheather, Simon; McKean, Joseph; Small, Christopher; Wood, Andrew (1999). "Multivariate L-estimation". TEST (Springer Berlin / Heidelberg) (2): 255– 317. doi:10.1007/BF02595872.