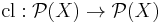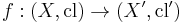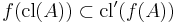Kuratowski closure axioms

In topology and related branches of mathematics, the Kuratowski closure axioms are a set of axioms which can be used to define a topological structure on a set. They are equivalent to the more commonly used open set definition. They were first introduced by Kazimierz Kuratowski, in a slightly different form that applied only to Hausdorff spaces.

A similar set of axioms can be used to define a topological structure using only the dual notion of interior operator.

Contents

Definition

A topological space 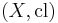(X,\operatorname{cl}) is a set X with a function

\operatorname{cl}:\mathcal{P}(X) \to \mathcal{P}(X)

called the closure operator where 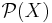\mathcal{P}(X) is the power set of X.

The closure operator has to satisfy the following properties for all 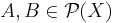A, B\in\mathcal{P}(X)

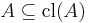  1. A \subseteq \operatorname{cl}(A) \! (Extensivity)
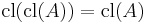  2. \operatorname{cl}(\operatorname{cl}(A)) = \operatorname{cl}(A) \! (Idempotence)
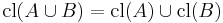  3. \operatorname{cl}(A \cup B) = \operatorname{cl}(A) \cup \operatorname{cl}(B) \! (Preservation of binary unions)
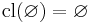  4. \operatorname{cl}(\varnothing) = \varnothing \! (Preservation of nullary unions)

If the second axiom, that of idempotence, is relaxed, then the axioms define a preclosure operator.

Notes

By induction, Axioms (3) and (4) are equivalent to the single statement

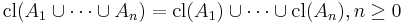\operatorname{cl}(A_{1} \cup \cdots \cup A_{n}) = \operatorname{cl}(A_{1}) \cup \cdots \cup \operatorname{cl}(A_{n}), n \geq 0 \! (Preservation of finitary unions).

Recovering topological definitions

A function between two topological spaces

f:(X,\operatorname{cl}) \to (X',\operatorname{cl}')

is called continuous if for all subsets A of X

f(\operatorname{cl}(A)) \subset \operatorname{cl}'(f(A))

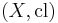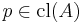
A point p is called close to A in (X,\operatorname{cl}) if p\in \operatorname{cl}(A)

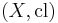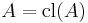A is called closed in (X,\operatorname{cl}) if A=\operatorname{cl}(A). In other words the closed sets of X are the fixed points of the closure operator.

If one takes an "open set" to be a set whose complement is closed, then the family of all open sets forms a topology. Conversely, any topology can be induced in this way by the correct choice of closure operator.

See also