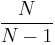Kuder-Richardson Formula 20
In statistics, the Kuder-Richardson Formula 20 (KR-20) first published in 1937 is a measure of internal consistency reliability for measures with dichotomous choices. It is analogous to Cronbach's α, except Cronbach's α is also used for non-dichotomous (continuous) measures. [1] A high KR-20 coefficient (e.g., >0.90) indicates a homogeneous test.
Values can range from 0.00 to 1.00 (sometimes expressed as 0 to 100), with high values indicating that the examination is likely to correlate with alternate forms (a desirable characteristic). The KR20 may be affected by difficulty of the test, the spread in scores and the length of the examination.
In the case when scores are not tau-equivalent (for example when there is not homogeneous but rather examination items of increasing difficulty) then the KR-20 is an indication of the lower bound of internal consistency (reliability).
where K is the length of the test and where the variance for the denominator is
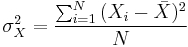 .
.
If it is important to use unbiased operators then the Sum of Squares should be divided by degrees of freedom (N − 1) and the probabilities are multiplied by
Since Cronbach's α was published in 1951, there has been no known advantage to KR-20 over Cronbach. KR-20 is seen as a derivative of the Cronbach formula, with the advantage to Cronbach that it can handle both dichotomous and continuous variables.
References
- ^ Cortina, J.M., (1993). What Is Coefficient Alpha? An Examination of Theory and Applications. Journal of Applied Psychology, 78(1), 98-104.
![\alpha={K\over{K-1}}{[{1-{\sum_{i=1}^K{p_{i}q_{i}}\over\sigma^{2}_{X}}}]}](/2012-wikipedia_en_all_nopic_01_2012/I/ebb476f4b890065e64221d2e560bff1a.png)