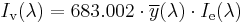Candela
The candela ( /kænˈdɛlə/ or /kænˈdiːlə/; symbol: cd) is the SI base unit of luminous intensity; that is, power emitted by a light source in a particular direction, weighted by the luminosity function (a standardized model of the sensitivity of the human eye to different wavelengths, also known as the luminous efficiency function[4][5]). A common candle emits light with a luminous intensity of roughly one candela. If emission in some directions is blocked by an opaque barrier, the emission would still be approximately one candela in the directions that are not obscured.
The word candela means candle in Latin, as well as in many modern languages.
Contents |
Definition
Like other SI base units, the candela has an operational definition—it is defined by a description of a physical process that will produce one candela of luminous intensity. Since the 16th General Conference on Weights and Measures (CGPM) in 1979, the candela has been defined as:[6]
The candela is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540×1012 hertz and that has a radiant intensity in that direction of 1⁄683 watt per steradian.
The definition describes how to produce a light source that (by definition) emits one candela. Such a source could then be used to calibrate instruments designed to measure luminous intensity.
The candela is sometimes still called by the old name candle,[7] such as in foot-candle and the modern definition of candlepower.
Explanation
The frequency chosen is in the visible spectrum near green, corresponding to a wavelength of about 555 nanometers. The human eye is most sensitive to this frequency, when adapted for bright conditions. At other frequencies, more radiant intensity is required to achieve the same luminous intensity, according to the frequency response of the human eye. The luminous intensity for light of a particular wavelength λ is given by
where Iv(λ) is the luminous intensity in candelas, Ie(λ) is the radiant intensity in W/sr and 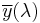 is the standard luminosity function. If more than one wavelength is present (as is usually the case), one must sum or integrate over the spectrum of wavelengths present to get the total luminous intensity.
is the standard luminosity function. If more than one wavelength is present (as is usually the case), one must sum or integrate over the spectrum of wavelengths present to get the total luminous intensity.
Examples
A common candle emits light with roughly 1 cd luminous intensity. A 25 W compact fluorescent light bulb puts out around 1700 lumens; if that light is radiated equally in all directions, it will have an intensity of around 135 cd. Focused into a 20° beam, it will have an intensity of around 18 000 cd.
The luminous intensity of light-emitting diodes is measured in millicandela (mcd), or thousandths of a candela. Indicator LEDs are typically in the 50 mcd range; "ultra-bright" LEDs can reach 15 000 mcd, or higher.
Origin
Prior to 1948, various standards for luminous intensity were in use in a number of countries. These were typically based on the brightness of the flame from a "standard candle" of defined composition, or the brightness of an incandescent filament of specific design. One of the best-known of these was the English standard of candlepower. One candlepower was the light produced by a pure spermaceti candle weighing one sixth of a pound and burning at a rate of 120 grains per hour. Germany, Austria and Scandinavia used the Hefnerkerze, a unit based on the output of a Hefner lamp.[8]
It became clear that a better-defined unit was needed. The Commission Internationale de l'Éclairage (International Commission on Illumination) and the CIPM proposed a “new candle” based on the luminance of a Planck radiator (a black body) at the temperature of freezing platinum. The value of the new unit was chosen to make it similar to the earlier unit candlepower. The decision was promulgated by the CIPM in 1946:
The value of the new candle is such that the brightness of the full radiator at the temperature of solidification of platinum is 60 new candles per square centimetre.[9]
It was then ratified in 1948 by the 9th CGPM which adopted a new name for this unit, the candela. In 1967 the 13th CGPM removed the term "new candle" and gave an amended version of the candela definition, specifying the atmospheric pressure applied to the freezing platinum:
The candela is the luminous intensity, in the perpendicular direction, of a surface of 1 / 600 000 square metre of a black body at the temperature of freezing platinum under a pressure of 101 325 newtons per square metre.[10]
In 1979, because of the difficulties in realizing a Planck radiator at high temperatures and the new possibilities offered by radiometry, the 16th CGPM adopted the modern definition of the candela.[11] The arbitrary (1/683) term was chosen so that the new definition would exactly match the old definition. Although the candela is now defined in terms of the second (an SI base unit) and the watt (a derived SI unit), the candela remains a base unit of the SI system, by definition.[12]
SI photometric light units
| Quantity | Symbol[nb 1] | SI unit | Symbol | Dimension | Notes | |||
|---|---|---|---|---|---|---|---|---|
| Luminous energy | Qv [nb 2] | lumen second | lm⋅s | T⋅J | units are sometimes called talbots | |||
| Luminous flux | Φv [nb 2] | lumen (= cd⋅sr) | lm | J | also called luminous power | |||
| Luminous intensity | Iv | candela (= lm/sr) | cd | J [nb 3] | an SI base unit, luminous flux per unit solid angle | |||
| Luminance | Lv | candela per square metre | cd/m2 | L−2⋅J | units are sometimes called nits | |||
| Illuminance | Ev | lux (= lm/m2) | lx | L−2⋅J | used for light incident on a surface | |||
| Luminous emittance | Mv | lux (= lm/m2) | lx | L−2⋅J | used for light emitted from a surface | |||
| Luminous exposure | Hv | lux second | lx⋅s | L−2⋅T⋅J | ||||
| Luminous energy density | ωv | lumen second per metre3 | lm⋅s⋅m−3 | L−3⋅T⋅J | ||||
| Luminous efficacy | η [nb 2] | lumen per watt | lm/W | M−1⋅L−2⋅T3⋅J | ratio of luminous flux to radiant flux | |||
| Luminous efficiency | V | 1 | also called luminous coefficient | |||||
| See also: SI · Photometry · Radiometry | ||||||||
- ^ Standards organizations recommend that photometric quantities be denoted with a suffix "v" (for "visual") to avoid confusion with radiometric or photon quantities.
- ^ a b c Alternative symbols sometimes seen: W for luminous energy, P or F for luminous flux, and ρ or K for luminous efficacy.
- ^ "J" is the recommended symbol for the dimension of luminous intensity in the International System of Units.
Relationship between luminous intensity and luminous flux
If a source emits a known luminous intensity Iv (in candelas) in a well-defined cone, the total luminous flux Φv in lumens is given by
- Φv = Iv ⋅ 2π ⋅ (1 - cos(A/2)),
where A is the radiation angle of the lamp—the full vertex angle of the emission cone. For example, a lamp that emits 590 cd with a radiation angle of 40° emits about 223 lumens. See MR16 for emission angles of some common lamps.[13][14][15]
If the source emits light uniformly in all directions, the flux can be found by multiplying the intensity by 4π: a uniform 1 candela source emits 12.6 lumens.
References
- ^ CIE Scotopic luminosity curve (1951)
- ^ CIE (1931) 2-deg color matching functions
- ^ Judd–Vos modified CIE 2-deg photopic luminosity curve (1978)
- ^ a b Sharpe, Stockman, Jagla & Jägle (2005) 2-deg V*(l) luminous efficiency function
- ^ Wyzecki, G.; Stiles, W.S. (1982). Color Science: Concepts and Methods, Quantitative Data and Formulae (2nd ed. ed.). Wiley-Interscience. ISBN 0-471-02106-7.
- ^ "Base unit definitions: Candela". The NIST Reference on Constants, Units, and Uncertainty. http://physics.nist.gov/cuu/Units/candela.html. Retrieved 27 September 2010.
- ^ Merriam-Webster
- ^ "Hefner unit, or Hefner candle". Sizes.com. 30 May 2007. http://www.sizes.com/units/hefner.htm. Retrieved 25 February 2009.
- ^ Barry N. Taylor (1992). The Metric System: The International System of Units (SI). U. S. Department of Commerce. p. 18. ISBN 0-941375-74-9. http://books.google.com/books?id=y2-BDaoBVnwC&pg=PA18&dq=%22value+of+the+new+candle+is+such+that+the+brightness+of+the+full+radiator%22&as_brr=3&ei=elatR_S1FofgswPvu430BQ&sig=yl2AU7A-R1O9e5ZuEzuLwekiM2E. (NIST Special Publication 330, 1991 ed.)
- ^ 13th CGPM Resolution 5, CR, 104 (1967), and Metrologia, 4, 43–44 (1968).
- ^ 16th CGPM Resolution 3, CR, 100 (1979), and Metrologia, 16, 56 (1980).
- ^ "The photometric base unit – the candela" (pdf). SI Brochure. Bureau International des Poids et Mesures. 7 September 2007. http://www1.bipm.org/utils/en/pdf/SIApp2_cd_en.pdf.
- ^ Theory
- ^ Formulas
- ^ Online converter
|
||||||||||||||||||||