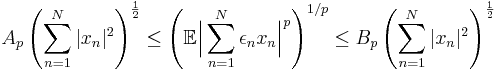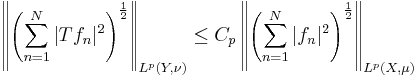Khintchine inequality
In mathematics, the Khintchine inequality, named after Aleksandr Khinchin and spelled in multiple ways in the Roman alphabet, is a theorem from probability, and is also frequently used in analysis. Heuristically, it says that if we pick  complex numbers
complex numbers 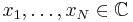 , and add them together each multiplied by a random sign
, and add them together each multiplied by a random sign 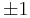 , then the expected value of its modulus, or the modulus it will be closest to on average, will be not too far off from
, then the expected value of its modulus, or the modulus it will be closest to on average, will be not too far off from  .
.
Contents |
Statement of theorem
Let 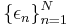 be i.i.d. random variables with
be i.i.d. random variables with 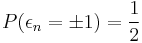 for every
for every 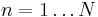 , i.e., a sequence with Rademacher distribution. Let
, i.e., a sequence with Rademacher distribution. Let 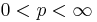 and let
and let 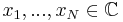 . Then
. Then
for some constants 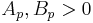 depending only on
depending only on  (see Expected value for notation). The sharp values of the constants
(see Expected value for notation). The sharp values of the constants 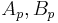 were found by Haagerup (Ref. 2; see Ref. 3 for a simpler proof).
were found by Haagerup (Ref. 2; see Ref. 3 for a simpler proof).
Uses in analysis
The uses of this inequality are not limited to applications in probability theory. One example of its use in analysis is the following: if we let  be a linear operator between two Lp spaces
be a linear operator between two Lp spaces 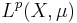 and
and 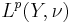 ,
, 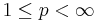 , with bounded norm
, with bounded norm 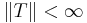 , then one can use Khintchine's inequality to show that
, then one can use Khintchine's inequality to show that
for some constant 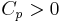 depending only on
depending only on  and
and 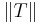 .
.
See also
References
- Thomas H. Wolff, "Lectures on Harmonic Analysis". American Mathematical Society, University Lecture Series vol. 29, 2003. ISBN 0-8218-3449-5
- Uffe Haagerup, "The best constants in the Khintchine inequality", Studia Math. 70 (1981), no. 3, 231–283 (1982).
- Fedor Nazarov and Anatoliy Podkorytov, "Ball, Haagerup, and distribution functions", Complex analysis, operators, and related topics, 247–267, Oper. Theory Adv. Appl., 113, Birkhäuser, Basel, 2000.