Kernelization
In computer science, a kernelization is an efficient algorithm that preprocesses instances of decision problems by mapping them to equivalent instances with a guaranteed upper bound on the size of the output, called the kernel of the instance. Kernelization is often achieved by applying a set of reduction rules that cut away parts of the instance that are easy to handle. Being a concept of parameterized complexity theory, it is natural to give the guarantee on the size of a kernel by comparing it with a parameter associated to the problem. Indeed, kernelization can be used as a technique for creating fixed-parameter tractable algorithms.
Contents |
Example: Vertex Cover
The standard example for a kernelization algorithm is the kernelization of the vertex cover problem by S. Buss.[1] In this problem, we are given a graph  and a number
and a number  and we want to know whether there is a vertex cover of size
and we want to know whether there is a vertex cover of size  . This problem is NP-hard and cannot be solved in polynomial time unless P=NP. However, some easy reduction rules for this problem exist:
. This problem is NP-hard and cannot be solved in polynomial time unless P=NP. However, some easy reduction rules for this problem exist:
Rule 1. If  is a vertex of degree
is a vertex of degree 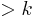 , remove
, remove  from the graph and decrease
from the graph and decrease  by one.
by one.
Any vertex cover of size  must contain
must contain  since otherwise all its neighbors would have to be picked to cover the incident edges.
since otherwise all its neighbors would have to be picked to cover the incident edges.
Rule 2. If  is an isolated vertex, remove it.
is an isolated vertex, remove it.
Isolated vertices cannot cover any edges and are not required for finding a vertex cover.
Rule 3. If more than 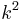 edges remain in the graph, it cannot contain a vertex cover of size
edges remain in the graph, it cannot contain a vertex cover of size  .
.
To see this, consider a vertex cover  of size
of size  . Since the degree of every vertex was reduced to at most
. Since the degree of every vertex was reduced to at most  by exhaustive application of the first rule, at most
by exhaustive application of the first rule, at most 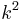 edges are incident to
edges are incident to  . On the other hand, all edges of
. On the other hand, all edges of  are incident to
are incident to  since it is a vertex cover, so
since it is a vertex cover, so  indeed has at most
indeed has at most 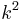 edges. Furthermore, since every vertex is either in
edges. Furthermore, since every vertex is either in  or adjacent to
or adjacent to  , the number of vertices is at most
, the number of vertices is at most 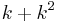 . Thus, we either know that the instance is a no-instance or we end up with a graph of at most
. Thus, we either know that the instance is a no-instance or we end up with a graph of at most 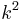 edges and
edges and 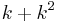 vertices.
vertices.
Kernels with fewer vertices
The most straightforward exhaustive search algorithm for the vertex cover problem runs in time roughly 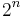 , where
, where  is the number of vertices. This algorithms just tries all subsets
is the number of vertices. This algorithms just tries all subsets 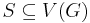 of the vertices and checks whether the given subset is a vertex cover. The algorithm can then check whether the graph has a vertex cover of size at most
of the vertices and checks whether the given subset is a vertex cover. The algorithm can then check whether the graph has a vertex cover of size at most  .
.
To speed up this and more advanced exhaustive search algorithms, it is desirable to first apply an efficient kernelization algorithm to the instance and run the exhaustive search on the thus created kernel. The running time of the overall algorithm is then dominated by the number of vertices in the kernel, for which reason the goal is to come up with kernels that have as few vertices as possible. For vertex cover, kernelization algorithms are known that produce kernels with at most 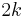 vertices.
vertices.
One kernelization algorithm that achieves the 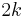 vertex bound exploits the half-integrality of the linear program relaxation of vertex cover due to Nemhauser and Trotter.[2] Another kernelization algorithm achieving that bound is based on what is known as the crown reduction rule and is based on alternating path arguments.[3]
vertex bound exploits the half-integrality of the linear program relaxation of vertex cover due to Nemhauser and Trotter.[2] Another kernelization algorithm achieving that bound is based on what is known as the crown reduction rule and is based on alternating path arguments.[3]
The currently best known kernelization algorithm in terms of the number of vertices is due to Lampis (2011) and achieves 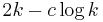 vertices for any fixed constant
vertices for any fixed constant  .
.
Kernel Lower Bounds
Given the many kernelization algorithms that exist and provide successive improvements, it is natural to ask for lower bounds on kernel sizes. Here the kernel sizes can be measured in terms of the number of vertices and in terms of the number of edges. It is suspected that the above mentioned kernelization algorithms for vertex cover are essentially optimal. In this case, kernels with 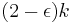 vertices or with
vertices or with 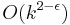 edges cannot be produced efficiently. Recently, it has been shown that the latter would imply that coNP
edges cannot be produced efficiently. Recently, it has been shown that the latter would imply that coNP 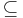 NP/poly,[4] which is a statement in complexity theory that is generally believed to be false.
NP/poly,[4] which is a statement in complexity theory that is generally believed to be false.
Definition
In the literature, there is no clear consensus on how kernelization should be formally defined and there are subtle differences in the uses of that expression.
Downey-Fellows Notation
In the Notation of Downey & Fellows (1999), a parameterized problem is a subset 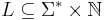 .
.
A kernelization for a parameterized problem  is an algorithm that takes an instance
is an algorithm that takes an instance 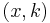 and maps it in time polynomial in
and maps it in time polynomial in 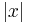 and
and  to an instance
to an instance 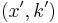 such that
such that
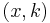 is in
is in  if and only if
if and only if 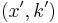 is in
is in  ,
,- the size of
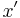 is bounded by a function
is bounded by a function  in
in  , and
, and 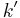 is bounded by a function in
is bounded by a function in  .
.
The output 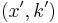 of kernelization is called a kernel. In this general context, the size of the string
of kernelization is called a kernel. In this general context, the size of the string 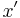 just refers to its length. Some authors prefer to use the number of vertices or the number of edges as the size measure in the context of graph problems.
just refers to its length. Some authors prefer to use the number of vertices or the number of edges as the size measure in the context of graph problems.
Flum-Grohe Notation
In the Notation of Flum & Grohe (2006, p. 437), a parameterized problem consists of a decision problem 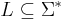 and a function
and a function 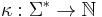 , the parameterization. The parameter of an instance
, the parameterization. The parameter of an instance  is the number
is the number 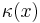 .
.
A kernelization for a parameterized problem  is an algorithm that takes an instance
is an algorithm that takes an instance  with parameter
with parameter  and maps it in polynomial time to an instance
and maps it in polynomial time to an instance  such that
such that
 is in
is in  if and only if
if and only if  is in
is in  and
and- the size of
 is bounded by a function
is bounded by a function  in
in  .
.
Note that in this notation, the bound on the size of  implies that the parameter of
implies that the parameter of  is also bounded by a function in
is also bounded by a function in  .
.
The function  is often referred to as the size of the kernel. If
is often referred to as the size of the kernel. If 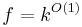 , it is said that
, it is said that  admits a polynomial kernel. Similarly, for
admits a polynomial kernel. Similarly, for 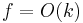 , the problem admits linear kernel.
, the problem admits linear kernel.
Kernelizability and fixed-parameter tractability are equivalent
A problem is fixed-parameter tractable if and only if it is kernelizable (with a computable size bound on the kernels) and decidable.
That a kernelizable and decidable problem is fixed-parameter tractable, can be seen from the definition above. Use the kernelization algorithm, which uses 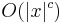 time for some c, and then solve the output from the kernelization in time
time for some c, and then solve the output from the kernelization in time 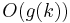 for some function g, which is finite, because the problem is decidable. The total running time is
for some function g, which is finite, because the problem is decidable. The total running time is 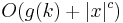 . The other direction, that a fixed-parameter tractable problem is kernelizable and decidable is a bit more involved. We will assume that the question is non-trivial, such that there is at least one instance that is in the language, called
. The other direction, that a fixed-parameter tractable problem is kernelizable and decidable is a bit more involved. We will assume that the question is non-trivial, such that there is at least one instance that is in the language, called 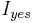 , and at least one instance that is not in the language, called
, and at least one instance that is not in the language, called 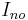 . Assume the input is (x, k), and that there exists an algorithm that runs in time
. Assume the input is (x, k), and that there exists an algorithm that runs in time 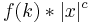 . We will now construct a kernelization algorithm, by finding in polynomial time an instance (x', k) where |x'| is bounded by k. If the size of x is less than f(k) we can just return (x, k). Otherwise, run the algorithm that proves the problem is fixed-parameter tractable and if the answer is yes, return
. We will now construct a kernelization algorithm, by finding in polynomial time an instance (x', k) where |x'| is bounded by k. If the size of x is less than f(k) we can just return (x, k). Otherwise, run the algorithm that proves the problem is fixed-parameter tractable and if the answer is yes, return 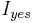 , otherwise return
, otherwise return 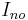 . The latter is ok because when
. The latter is ok because when 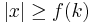 , we get also that
, we get also that 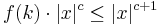 .
.
More Examples
- Vertex Cover: The vertex cover problem has kernels with at most
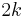 vertices and
vertices and 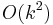 edges.[5] Furthermore, for any
edges.[5] Furthermore, for any 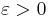 , vertex cover does not have kernels with
, vertex cover does not have kernels with 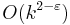 edges unless
edges unless 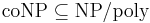 .[4] The vertex cover problems in
.[4] The vertex cover problems in  -uniform hypergraphs has kernels with
-uniform hypergraphs has kernels with 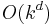 edges using the sunflower lemma, and it does not have kernels of size
edges using the sunflower lemma, and it does not have kernels of size 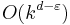 unless
unless 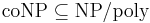 .[4]
.[4] - Feedback Vertex Set: The feedback vertex set problem has kernels with
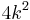 vertices and
vertices and 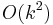 edges[6]. Furthermore, it does not have kernels with
edges[6]. Furthermore, it does not have kernels with 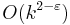 edges unless
edges unless 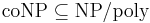 .[4]
.[4] - k-Path: The k-path problem is to decide whether a given graph has a path of length at least
 . This problem has kernels of size exponential in
. This problem has kernels of size exponential in  , and it does not have kernels of size polynomial in
, and it does not have kernels of size polynomial in  unless
unless 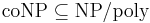 .[7]
.[7] - Bidimensional problems: Many parameterized versions of bidimensional problems have linear kernels on planar graphs, and more generally, on graphs excluding some fixed graph as a minor.[8]
Notes
- ^ This unpublished observation is acknowledged in a paper of Buss & Goldsmith (1993)
- ^ Flum & Grohe (2006)
- ^ Flum & Grohe (2006) give a kernel based on the crown reduction that has
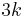 vertices. The
vertices. The 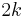 vertex bound is a bit more involved and folklore.
vertex bound is a bit more involved and folklore. - ^ a b c d Dell & van Melkebeek (2010)
- ^ Chen, Kanj & Jia (2001)
- ^ Thomassé (2010)
- ^ Bodlaender et al. (2009)
- ^ Fomin et al. (2010)
References
- Abu-Khzam, Faisal N.; Collins, Rebecca L.; Fellows, Michael R.; Langston, Michael A.; Suters, W. Henry; Symons, Chris T. (2004), Kernelization Algorithms for the Vertex Cover Problem: Theory and Experiments, University of Tennessee, http://www.cs.utk.edu/~langston/projects/papers/ACFLSS.pdf
- Bodlaender, Hans L.; Downey, Rod G.; Fellows, Michael R.; Hermelin, Danny (2009), On problems without polynomial kernels, , J. Comput. Syst. Sci. 75(8): 423–434.
- Buss, Jonathan F.; Goldsmith, Judy (1993), "Nondeterminism within P", SIAM Journal on Computing 22 (3): 560–572
- Chen, Jianer; Kanj, Iyad A.; Jia, Weijia (2001), Further Observations and Further Improvements, , J.Algorithms 41(2): 280–301.
- Dell, Holger; van Melkebeek, Dieter (2010), "Satisfiability allows no nontrivial sparsification unless the polynomial-time hierarchy collapses", STOC 2010, pp. 251–260.
- Downey, Rod G.; Fellows, Michael R. (1999), Parameterized Complexity, Springer, ISBN 0-387-94883-X, http://www.springer.com/sgw/cda/frontpage/0,11855,5-0-22-1519914-0,00.html?referer=www.springer.de%2Fcgi-bin%2Fsearch_book.pl%3Fisbn%3D0-387-94883-X
- Flum, Jörg; Grohe, Martin (2006), Parameterized Complexity Theory, Springer, ISBN 978-3-540-29952-3, http://www.springer.com/east/home/generic/search/results?SGWID=5-40109-22-141358322-0, retrieved 2010-03-05
- Fomin, Fedor V.; Lokshtanov, Daniel; Saurabh, Saket; Thilikos, Dimitrios M. (2010), "Bidimensionality and Kernels", 21st ACM-SIAM Symposium on Discrete Algorithms (SODA 2010), pp. 503–510.
- Lampis, Michael (2011), A kernel of order
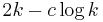 for vertex cover, , Information Processing Letters (Elsevier) 111 (23–24): 1089–1091, doi:10.1016/j.ipl.2011.09.003.
for vertex cover, , Information Processing Letters (Elsevier) 111 (23–24): 1089–1091, doi:10.1016/j.ipl.2011.09.003. - Thomassé, Stéphan (2010), A
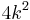 kernel for feedback vertex set, , ACM Transactions on Algorithms 6(2).
kernel for feedback vertex set, , ACM Transactions on Algorithms 6(2). - Niedermeier, Rolf (2006), Invitation to Fixed-Parameter Algorithms, Oxford University Press, ISBN 0-19-856607-7, http://www.oup.com/uk/catalogue/?ci=9780198566076