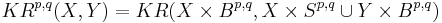KR-theory

In mathematics, KR-theory is a variant of topological K-theory defined for spaces with an involution. It was introduced by Atiyah (1966), motivated by applications to the Atiyah–Singer index theorem for real elliptic operators.

Definition

A real space is a defined to be a topological space with an involution. A real vector bundle over a real space X is defined to be a complex vector bundle E over X that is also a real space, such that the natural maps from E to X and from C×E to E commute with the involution, where the involution acts as complex conjugation on C. (This differs from the notion of a complex vector bundle in the category of Z/2Z spaces, where the involution acts trivially on C.) The group KR(X) is the Grothendieck group of finite dimensional real vector bundles over the real space X.

Periodicity

The periodicity theorem for KR states that KR^p,q = KR^p+1,q+1, where KR^p,q is suspension with respect to R^p,q = R^q + iR^p (with a switch in the order of p and q), given by

$KR^{p,q}(X,Y) = KR(X\times B^{p,q},X\times S^{p,q}\cup Y\times B^{p,q})$

and B^p,q, S^p,q are the unit ball and sphere in R^p,q.

References

Atiyah, Michael Francis (1966), "K-theory and reality", The Quarterly Journal of Mathematics. Oxford. Second Series 17 (1): 367–386, doi:10.1093/qmath/17.1.367, ISSN 0033-5606, MR 0206940, http://qjmath.oxfordjournals.org/cgi/reprint/17/1/367