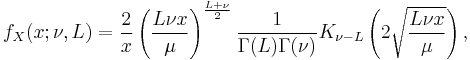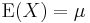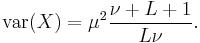K-distribution

The K-distribution is a probability distribution that arises as the consequence of a statistical or probabilistic model used in Synthetic Aperture Radar (SAR) imagery. The K distribution is formed by compounding two separate probability distributions, one representing the radar cross-section, and the other representing speckle that is a characteristic of coherent imaging.

The model used to represent the observed intensity X, involves compounding two gamma distributions. In each case a reparameterisation of the usual form of the family of gamma distributions is used, such that the parameters are:

  • the mean of the distribution, and
  • the usual shape parameter.

Contents

Density

The model is that X has a gamma distribution with mean σ and shape parameter L, with σ being treated as a random variable having another gamma distribution, this time with mean μ and shape parameter ν. The result is that X has the following density function (x > 0):[1]

f_X(x;\nu,L)= \frac{2}{x} \left( \frac{L \nu x}{\mu} \right)^\frac{L%2B\nu}{2} \frac{1}{\Gamma(L)\Gamma(\nu)} K_{\nu-L} \left( 2 \sqrt{\frac{L \nu x}{\mu} } \right),

where K is a modified Bessel function of the second kind. In this derivation, the K-distribution is a compound probability distribution. It is also a product distribution:[1] it is the distribution of the product of two independent random variables, one having a gamma distribution with mean 1 and shape parameter L, the second having a gamma distribution with mean μ and shape parameter ν.

This distribution derives from a paper by Jakeman and Pusey (1978).

Moments

The mean and variance are given[1] by

\operatorname{E}(X)= \mu
\operatorname{var}(X)= \mu^2 \frac{ \nu%2BL%2B1}{L \nu} .

Other properties

All the properties of the distribution are symmetric in L and ν.[1]

Notes

  1. ^ a b c d Redding (1999)

Sources

Further reading