Jordan's totient function

In number theory, Jordan's totient function 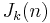$J_k(n)$ of a positive integer n is the number of k-tuples of positive integers all less than or equal to n that form a coprime (k + 1)-tuple together with n. This is a generalisation of Euler's totient function, which is J₁. The function is named after Camille Jordan.

1 Definition
2 Properties
3 Order of matrix groups
4 Notes
5 References
6 External links

Definition

Jordan's totient function is multiplicative and may be evaluated as

$J_k(n)=n^k \prod_{p|n}\left(1-\frac{1}{p^k}\right) .\,$

Properties

$\sum_{d | n } J_k(d) = n^k. \,$

which may be written in the language of Dirichlet convolutions as

$J_k(n) \star 1 = n^k\,$

and via Möbius inversion as

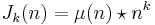$J_k(n) = \mu(n) \star n^k$ .

Since the Dirichlet generating function of μ is 1/ζ(s) and the Dirichlet generating function of n^k is ζ(s-k), the series for J_k becomes

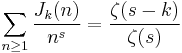$\sum_{n\ge 1}\frac{J_k(n)}{n^s} = \frac{\zeta(s-k)}{\zeta(s)}$ .

The average order of J_k(n) is c n^k for some c.

The Dedekind psi function is

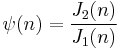$\psi(n) = \frac{J_2(n)}{J_1(n)}$ ,

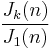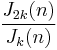and by inspection of the definition (recognizing that each factor in the product over the primes is a cyclotomic polynomial of p^-k), the arithmetic functions defined by $\frac{J_k(n)}{J_1(n)}$ or $\frac{J_{2k}(n)}{J_k(n)}$ can also be shown to be integer-valued multiplicative functions.

$\sum_{\delta\mid n}\delta^sJ_r(\delta)J_s\left(\frac{n}{\delta}\right) = J_{r%2Bs}(n)$ ^[1]

Order of matrix groups

The general linear group of matrices of order m over Z_n has order^[2]

$|GL(m,Z_n)|=n^{\frac{m(m-1)}{2}}\prod_{k=1}^m J_k(n).$

The special linear group of matrices of order m over Z_n has order

$|SL(m,Z_n)|=n^{\frac{m(m-1)}{2}}\prod_{k=2}^m J_k(n).$

The symplectic group of matrices of order m over Z_n has order

$|Sp(2m,Z_n)|=n^{m^2}\prod_{k=1}^m J_{2k}(n).$

The first two formulas were discovered by Jordan.

Notes

^ Holden et al in external links The formula is Gegenbauer's
^ All of these formulas are from Andrici and Priticari in #external links

References

L. E. Dickson (1919, repr.1971). History of the Theory of Numbers I. Chelsea. p. 147. ISBN 0-8284-0086-5.
M. Ram Murty (2001). Problems in Analytic Number Theory. Graduate Texts in Mathematics. 206. Springer-Verlag. p. 11. ISBN 0-387-95143-1.

External links

Dorin Andrica and Mihai Piticari On some Extensions of Jordan's arithmetical Functions

Matthew Holden, Michael Orrison, Michael Varble Yet another Generalization of Euler's Totient Function

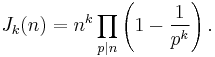
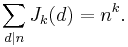
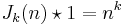
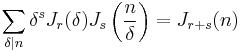
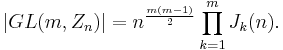
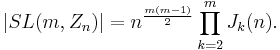
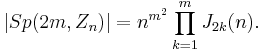
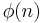Totient function

Euler's totient function $\phi(n)$ · Jordan's totient function $J_k(n)$ · Nontotient · Noncototient · Highly totient number · Sparsely totient number · Highly cototient number