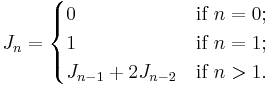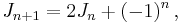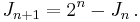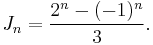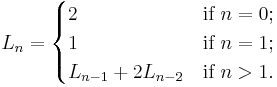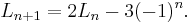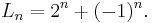Jacobsthal number

In mathematics, the Jacobsthal numbers are an integer sequence named after the German mathematician Ernst Jacobsthal. Like the related Fibonacci numbers, they are a specific type of Lucas sequence $U_n(P,Q)$ for which P = 1, and Q = −2^[1]—and are defined by a similar recurrence relation: in simple terms, the sequence starts with 0 and 1, then each following number is found by adding the number before it to twice the number before that. The first Jacobsthal numbers are:

0, 1, 1, 3, 5, 11, 21, 43, 85, 171, 341, 683, 1365, 2731, 5461, 10923, 21845, 43691, 87381, 174763, 349525, … (sequence A001045 in OEIS)

Jacobsthal numbers

Jacobsthal numbers are defined by the recurrence relation:

$J_n = \begin{cases} 0 & \mbox{if } n = 0; \\ 1 & \mbox{if } n = 1; \\ J_{n-1} %2B 2J_{n-2} & \mbox{if } n > 1. \\ \end{cases}$

The next Jacobsthal number is also given by the recursion formula:

$J_{n%2B1} = 2J_n %2B (-1)^n \, ,$

or by:

$J_{n%2B1} = 2^n - J_n \, .$

The first recursion formula above is also satisfied by the powers of 2.

The Jacobsthal number at a specific point in the sequence may be calculated directly using the closed-form equation:^[2]

$J_n = \frac{2^n - (-1)^n} 3.$

The generating function for the Jacobsthal numbers is

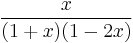$\frac{x}{(1%2Bx)(1-2x)}$ .

Jacobsthal-Lucas numbers

Jacobsthal-Lucas numbers retain the recurrence relation, L_n-1 + 2L_n-2, of Jacobsthal numbers, but use the starting conditions of the Lucas numbers, i.e. L₀ = 2, and L₁ = 1; they are defined by the recurrence relation:

$L_n = \begin{cases} 2 & \mbox{if } n = 0; \\ 1 & \mbox{if } n = 1; \\ L_{n-1} %2B 2L_{n-2} & \mbox{if } n > 1. \\ \end{cases}$

The following Jacobsthal-Lucas number also satisfies:^[3]

$L_{n%2B1} = 2L_n - 3(-1)^n. \,$

The Jacobsthal-Lucas number at a specific point in the sequence may be calculated directly using the closed-form equation:^[3]

$L_n = 2^n %2B (-1)^n. \,$

The first Jacobsthal-Lucas numbers are:

2, 1, 5, 7, 17, 31, 65, 127, 257, 511, 1025, 2047, 4097, 8191, 16385, 32767, 65537, 131071, 262145, 524287, 1048577, … (sequence A014551 in OEIS)

References

^ Weisstein, Eric W. (2006-05-15). "Jacobsthal Number". Wolfram Mathworld. http://mathworld.wolfram.com/JacobsthalNumber.html. Retrieved 2007-10-03.
^ Sloane's A001045 : Jacobsthal sequence. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
^ ^a ^b Sloane's A014551 : Jacobsthal-Lucas numbers. The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.