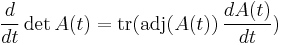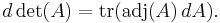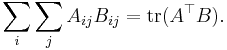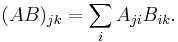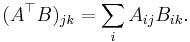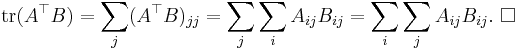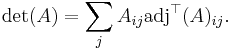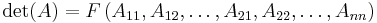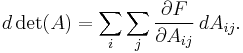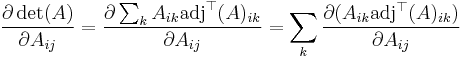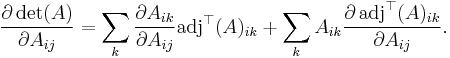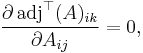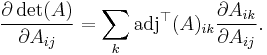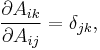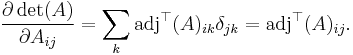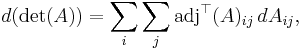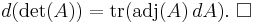Jacobi's formula

In matrix calculus, Jacobi's formula expresses the derivative of the determinant of a matrix A in terms of the adjugate of A and the derivative of A.^[1] If A is a differentiable map from the real numbers to n × n matrices,

$\frac{d}{dt} \det A(t) = \mathrm{tr} (\mathrm{adj}(A(t)) \, \frac{dA(t)}{dt})\,$

Equivalently, if dA stands for the differential of A, the formula is

$d \det (A) = \mathrm{tr} (\mathrm{adj}(A) \, dA).$

It is named after the mathematician C.G.J. Jacobi.

Derivation

We first prove a preliminary lemma:

Lemma. Let A and B be a pair of square matrices of the same dimension n. Then

$\sum_i \sum_j A_{ij} B_{ij} = \mathrm{tr} (A^\top B).$

Proof. The product AB of the pair of matrices has components

$(AB)_{jk} = \sum_i A_{ji} B_{ik}.\,$

Replacing the matrix A by its transpose A^T is equivalent to permuting the indices of its components:

$(A^\top B)_{jk} = \sum_i A_{ij} B_{ik}.$

The result follows by taking the trace of both sides:

$\mathrm{tr} (A^\top B) = \sum_j (A^\top B)_{jj} = \sum_j \sum_i A_{ij} B_{ij} = \sum_i \sum_j A_{ij} B_{ij}.\ \square$

Theorem. (Jacobi's formula) For any differentiable map A from the real numbers to n × n matrices,

$d \det (A) = \mathrm{tr} (\mathrm{adj}(A) \, dA).$

Proof. Laplace's formula for the determinant of a matrix A can be stated as

$\det(A) = \sum_j A_{ij} \mathrm{adj}^\top (A)_{ij}.$

Notice that the summation is performed over some arbitrary row i of the matrix.

The determinant of A can be considered to be a function of the elements of A:

$\det(A) = F\,(A_{11}, A_{12}, \ldots , A_{21}, A_{22}, \ldots , A_{nn})$

so that, by the chain rule, its differential is

$d \det(A) = \sum_i \sum_j {\partial F \over \partial A_{ij}} \,dA_{ij}.$

This summation is performed over all n×n elements of the matrix.

To find ∂F/∂A_ij consider that on the right hand side of Laplace's formula, the index i can be chosen at will. (In order to optimize calculations: Any other choice would eventually yield the same result, but it could be much harder). In particular, it can be chosen to match the first index of ∂ / ∂A_ij:

${\partial \det(A) \over \partial A_{ij}} = {\partial \sum_k A_{ik} \mathrm{adj}^\top(A)_{ik} \over \partial A_{ij}} = \sum_k {\partial (A_{ik} \mathrm{adj}^\top(A)_{ik}) \over \partial A_{ij}}$

Thus, by the product rule,

${\partial \det(A) \over \partial A_{ij}} = \sum_k {\partial A_{ik} \over \partial A_{ij}} \mathrm{adj}^\top(A)_{ik} %2B \sum_k A_{ik} {\partial \, \mathrm{adj}^\top(A)_{ik} \over \partial A_{ij}}.$

Now, if an element of a matrix A_ij and a cofactor adj^T(A)_ik of element A_ik lie on the same row (or column), then the cofactor will not be a function of A_ij, because the cofactor of A_ik is expressed in terms of elements not in its own row (nor column). Thus,